Strike it Out for Two

Here's a game to play with an adult!
 
 

How do you play?
You'll need an adult to play with.
You'll also need a number line from 0 to 20, like the one above. You can find some of these here.

Watch the video below which shows two people playing the first few turns of a game.

Can you work out how to play the game?  
What do you think the rules might be? 
How might someone win the game?

When you've talked about your ideas, carry on reading to check how to play:

The adult chooses a number on the line and crosses it out.
They then choose a second number and cross that out too.
Finally, the adult circles the sum or difference of the two numbers and writes down the calculation.

For example, the adult's go could look like this:



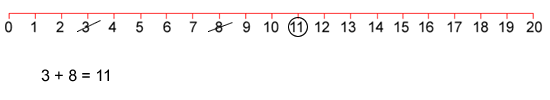
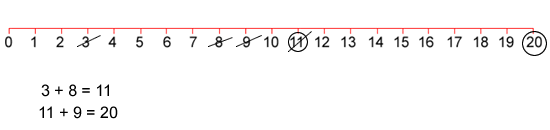
You must start by crossing off the number that the adult has just circled.
You then choose another number to cross out, and then circle a third number which is the sum or difference of the two crossed-off numbers.
You also writes down their calculation.

For example, once you have had a turn, the game could look like this:




Play continues in this way with each player starting with the number that has just been circled.

For example, the adult could then have a turn which left the game looking like this:



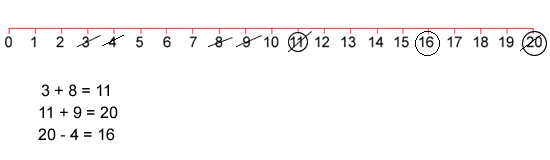
The winner of the game is the player who stops their opponent from being able to go.

What is your strategy for winning?
Can you cross out all the numbers in one game? How do you know?
What is the biggest number of numbers you can cross out?