Dicey Operations in Line for Two

Here's a game to play with an adult!




How do you play?
You'll need an adult to play with.
You'll need a scoring sheet, which could either be some squared paper or this sheet.
You'll also need a 1 to 6 dice, or even a 0 to 9 dice if you have one. You could use a spinner instead of a dice. (You could use our interactive dice/spinner.)

Take turns to throw the dice and decide which of your cells to fill. This can be done in two ways: either fill in each cell as you throw the dice or collect all your numbers and then decide where to place them.


Game 1

Each of you draw an addition grid like this:



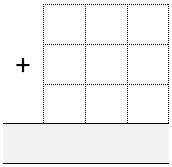
Throw the dice nine times each until all the cells are full.

Whoever has the sum closest to 1000 wins.

There are two possible scoring systems:

• A point for a win. The first person to reach 10 wins the game.
• Each player works out the difference between their result and 1000 after each round. They keep their running total. First to 5000 loses.

You can vary the target to make it easier or more difficult.

Game 2

Each of you draw a subtraction grid like this:



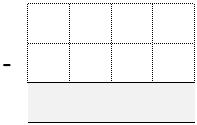
Throw the dice eight times each until all the cells are full.

Whoever has the difference closest to 1000 wins.

There are two possible scoring systems:

• A point for a win. The first person to reach 10 wins the game.
• Each player works out the difference between their result and 1000 after each round. They keep their running total. First to 5000 loses.

You can vary the target to make it easier or more difficult, perhaps including negative numbers as your target.

Game 3

Each of you draw a multiplication grid like this:



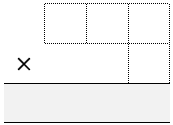
Throw the dice four times each until all the cells are full.

Whoever has the product closest to 1000 wins.

There are two possible scoring systems:

• A point for a win. The first person to reach 10 wins the game.
• Each player works out the difference between their result and 1000 after each round. They keep their running total. First to 5000 loses.

You can vary the target to make it easier or more difficult.

Game 4

Each of you draw a multiplication grid like this:



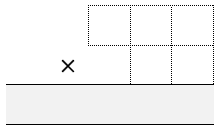
Throw the dice five times each until all the cells are full.


Whoever has the product closest to 10000 wins.

There are two possible scoring systems:

• A point for a win. The first person to reach 10 wins the game.
• Each player works out the difference between their result and 10000 after each round. They keep their running total. First to 10000 loses.

You can vary the target to make it easier or more difficult.

You could introduce a decimal point. The decimal point could take up one of the cells so the dice would only need to be thrown four times by each player. You will need to decide on an appropriate target.

Game 5



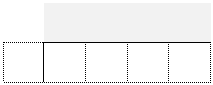
Each of you draw a division grid like this:

Throw the dice five times each until all the cells are full.

Whoever has the answer closest to 1000 wins.

There are two possible scoring systems:

• A point for a win. The first person to reach 10 wins the game.
• Each player works out the difference between their result and 1000 after each round. They keep their running total. First to 5000 loses.

You can vary the target to make it easier or more difficult.

Game 6

Each of you draw a division grid like this:



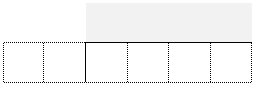
Throw the dice six times each until all the cells are full.

Whoever has the answer closest to 100 wins.

There are two possible scoring systems:

• A point for a win. The first person to reach 10 wins the game.
• Each player works out the difference between their result and 100 after each round. They keep their running total. First to 500 loses.

You can vary the target to make it easier or more difficult.
 

Why are some cells more significant than others?
How do you decide which targets are appropriate?
What are effective strategies for placing the numbers?
 

You may like to make use of this Score Sheet 

Click here for a poster of this problem.