Skip over navigation
Answer: $25$
Using few unknowns
first + (middle 3) = (middle 3) + last $\therefore$ first = last, so the numbers indicated are equal



The code is:
Repeat for the 5s:


The code is: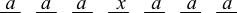
Fours: $3a+x=16$
Fives: $4a+x=19$
$\therefore a=3$
All seven: $6a+x = 2a + (4a+x) = 6+19=25$
Using seven unknowns
Let the $7$-digit code be $abcdefg$.
We know that
$(1)$ $a+b+c+d=16$
$(2)$ $b+c+d+e=16$
$(3)$ $c+d+e+f=16$
$(4)$ $d+e+f+g=16$
$(5)$ $a+b+c+d+e=19$
$(6)$ $b+c+d+e+f=19$
$(7)$ $c+d+e+f+g=19$
If we take equation $(1)$ away from equation $(5)$ we obtain $e=3$.
Similarly:
$(6)-(2)$ gives that $f=3$,
$(7)-(3)$ gives that $g=3$,
$(5)-(2)$ gives that $a=3$,
$(6)-(3)$ gives that $b=3$ and
$(7)-(4)$ gives that $c=3$.
Then using equation $(1)$ we find that $d=7$.
So the code is $3337333$ and the sum of the digits is $25$.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Adjacent Additions
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: $25$
Using few unknowns
first + (middle 3) = (middle 3) + last $\therefore$ first = last, so the numbers indicated are equal



The code is:

Repeat for the 5s:


The code is:
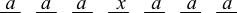
Fours: $3a+x=16$
Fives: $4a+x=19$
$\therefore a=3$
All seven: $6a+x = 2a + (4a+x) = 6+19=25$
Using seven unknowns
Let the $7$-digit code be $abcdefg$.
We know that
$(1)$ $a+b+c+d=16$
$(2)$ $b+c+d+e=16$
$(3)$ $c+d+e+f=16$
$(4)$ $d+e+f+g=16$
$(5)$ $a+b+c+d+e=19$
$(6)$ $b+c+d+e+f=19$
$(7)$ $c+d+e+f+g=19$
If we take equation $(1)$ away from equation $(5)$ we obtain $e=3$.
Similarly:
$(6)-(2)$ gives that $f=3$,
$(7)-(3)$ gives that $g=3$,
$(5)-(2)$ gives that $a=3$,
$(6)-(3)$ gives that $b=3$ and
$(7)-(4)$ gives that $c=3$.
Then using equation $(1)$ we find that $d=7$.
So the code is $3337333$ and the sum of the digits is $25$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Square It
Players take it in turns to choose a dot on the grid. The winner is the first to have four dots that can be joined to form a square.
Warmsnug Double Glazing
How have "Warmsnug" arrived at the prices shown on their windows? Which window has been given an incorrect price?

