Skip over navigation
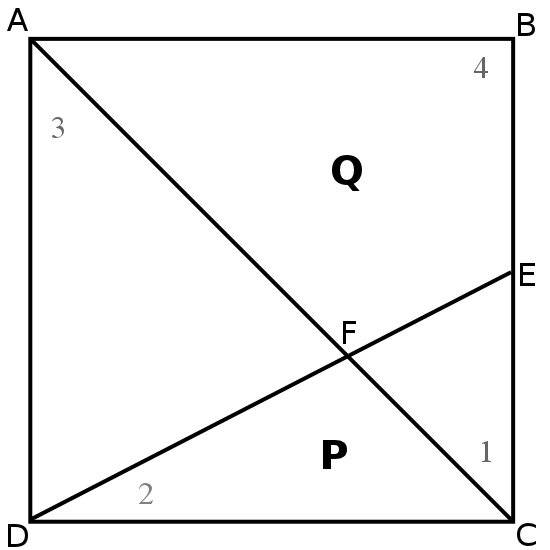
First, we label the corners of the square, the midpoint, and the point at which the two lines intersect $A$, $B$, $C$, $D$, $E$ and$F$ respectively. We also label the four triangles created within the square as 1, 2, 3 and 4.
Call the area of triangle a.
Angle $AFD$ is equal to angle $EFC$ as they are vertically opposite, and angle $FAD$ is equal to angle $FCD$ as they are alternate. So, triangles 1 and 3 are similar. As $E$ marks the midpoint of a side of the square, length $CE$ is half the value of length $AD$.
This means that the area of triangle 3 is equal to 4a, as its base and height are double that of triangle 1.
It also means that length $AF$ is equal to twice the value of length $FC$. If we let $AF$ be the base of triangle 3 and $FC$ be the base of triangle 2, then these triangles have the same height (equal to the perpendicular distance from $D$ to the line $AF$) so the area of triangle 2 is equal to half that of triangle 3 - that is, 2a.
As line $AC$ is a diagonal, the combined areas of triangles 2 and 3 is equal to half the area of the square. 4a + 2a = 6a, so the square has a total area of 12a. The combined area of triangle 1 and triangle 4 is then also 6a. As we have defined the area of triangle 1 as a, we then know that triangle 4 has an area of 5a.
As the ratio of $P:Q$ is simply the ratio area of triangle 2:area of triangle 4, we then know that this ratio is 2a:5a=2:5.
Cut-up Square
Age 14 to 16
ShortChallenge Level 
First, we label the corners of the square, the midpoint, and the point at which the two lines intersect $A$, $B$, $C$, $D$, $E$ and$F$ respectively. We also label the four triangles created within the square as 1, 2, 3 and 4.
Call the area of triangle a.
Angle $AFD$ is equal to angle $EFC$ as they are vertically opposite, and angle $FAD$ is equal to angle $FCD$ as they are alternate. So, triangles 1 and 3 are similar. As $E$ marks the midpoint of a side of the square, length $CE$ is half the value of length $AD$.
This means that the area of triangle 3 is equal to 4a, as its base and height are double that of triangle 1.
It also means that length $AF$ is equal to twice the value of length $FC$. If we let $AF$ be the base of triangle 3 and $FC$ be the base of triangle 2, then these triangles have the same height (equal to the perpendicular distance from $D$ to the line $AF$) so the area of triangle 2 is equal to half that of triangle 3 - that is, 2a.
As line $AC$ is a diagonal, the combined areas of triangles 2 and 3 is equal to half the area of the square. 4a + 2a = 6a, so the square has a total area of 12a. The combined area of triangle 1 and triangle 4 is then also 6a. As we have defined the area of triangle 1 as a, we then know that triangle 4 has an area of 5a.
As the ratio of $P:Q$ is simply the ratio area of triangle 2:area of triangle 4, we then know that this ratio is 2a:5a=2:5.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Bendy Quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.