Four Square

 
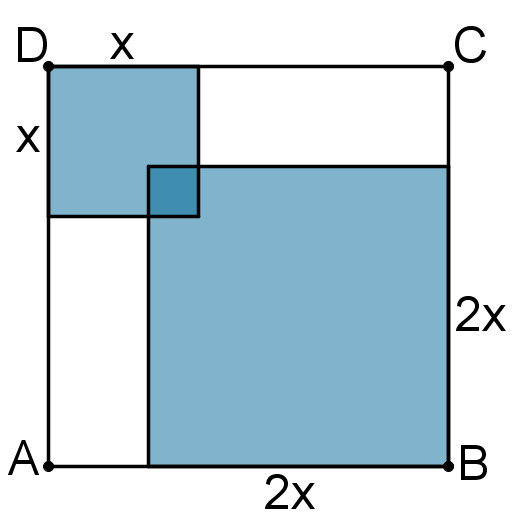
The large square has area $196 = 14^2$, so it has side-length $14$.

The ratio of the areas of the inner squares is $4 : 1$, so the ratio of their side-lengths is $2 : 1$.

Let the side-length of the larger inner square be $2x$, so that of the smaller is $x$.

The figure is symmetric about the diagonal AC and so the overlap of the two inner squares is also a square which therefore has side-length $1$.

Thus the vertical height can be written as $x + 2x - 1$.

Hence $3x - 1 = 14$ and so $x = 5$.

So the small shaded square has an area of $25$ and the large shaded square has an area of $100$.

Therefore, the total shaded area = $25 + 100 - 1 = 124$

Note also that the two unshaded rectangles have side-lengths of $14 - 2x$ and $14 - x$; that is $4$ and $9$.

So the total unshaded area is $36 \times 2 = 72$, and therefore the total shaded area is $196-72=124$