Skip over navigation
At each weighing we should compare two sets of coins where each set has the same number of coins. There are three outcomes:
In case 1, the fake coin is in the left-hand set, in case 2, the fake coin is in the right-hand set and in case 3 the fake coin is in neither set.
Consider the following flowchart. Each red/blue ellipse represents a weighing. If the left-hand set is heavier follow the red arrow, if the right-hand set is heavier follow the blue arrow and if the two sets are the same weight follow the purple arrow.
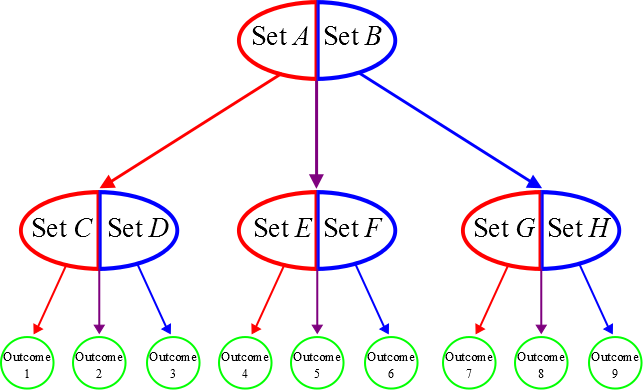
There are $9$ possible routes through the flowchart and so there are $9$ possible outcomes. At the end of the two weighings you could end up at any outcome and we want to be able to tell which coin is fake, so we can only test at most $9$ coins.
Can we test $9$ coins? Yes. Label the coins $1$,$2$,$3$,...,$9$ and see the diagram below.
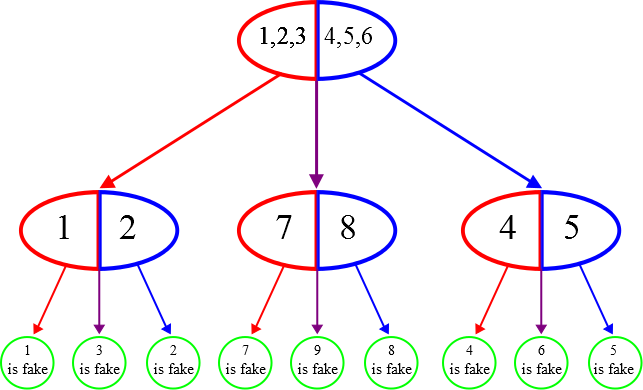
For example, if the set $1$,$2$,$3$ has the same weight as $4$,$5$,$6$ the the fake coin must be one of $7$,$8$,$9$.
If $7$ is heavier than $8$ then $7$ is fake, or
if $8$ is heavier than $7$ then $8$ is fake, or
if $7$ and $8$ are the same weight then $9$ is fake.
So the largest possible value for $N$ is $9$.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Spot the Fake
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
At each weighing we should compare two sets of coins where each set has the same number of coins. There are three outcomes:
- Left-hand set is heavier
- Right-hand set is heavier
- The sets have equal weight.
In case 1, the fake coin is in the left-hand set, in case 2, the fake coin is in the right-hand set and in case 3 the fake coin is in neither set.
Consider the following flowchart. Each red/blue ellipse represents a weighing. If the left-hand set is heavier follow the red arrow, if the right-hand set is heavier follow the blue arrow and if the two sets are the same weight follow the purple arrow.

There are $9$ possible routes through the flowchart and so there are $9$ possible outcomes. At the end of the two weighings you could end up at any outcome and we want to be able to tell which coin is fake, so we can only test at most $9$ coins.
Can we test $9$ coins? Yes. Label the coins $1$,$2$,$3$,...,$9$ and see the diagram below.

For example, if the set $1$,$2$,$3$ has the same weight as $4$,$5$,$6$ the the fake coin must be one of $7$,$8$,$9$.
If $7$ is heavier than $8$ then $7$ is fake, or
if $8$ is heavier than $7$ then $8$ is fake, or
if $7$ and $8$ are the same weight then $9$ is fake.
So the largest possible value for $N$ is $9$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Doodles
Draw a 'doodle' - a closed intersecting curve drawn without taking pencil from paper. What can you prove about the intersections?
Russian Cubes
I want some cubes painted with three blue faces and three red faces. How many different cubes can be painted like that?
Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?

