Play to 37

Thank you to everybody who sent us their solutions to this problem.

Ariana from Halstead Preparatory School in the UK sent in this explanation:

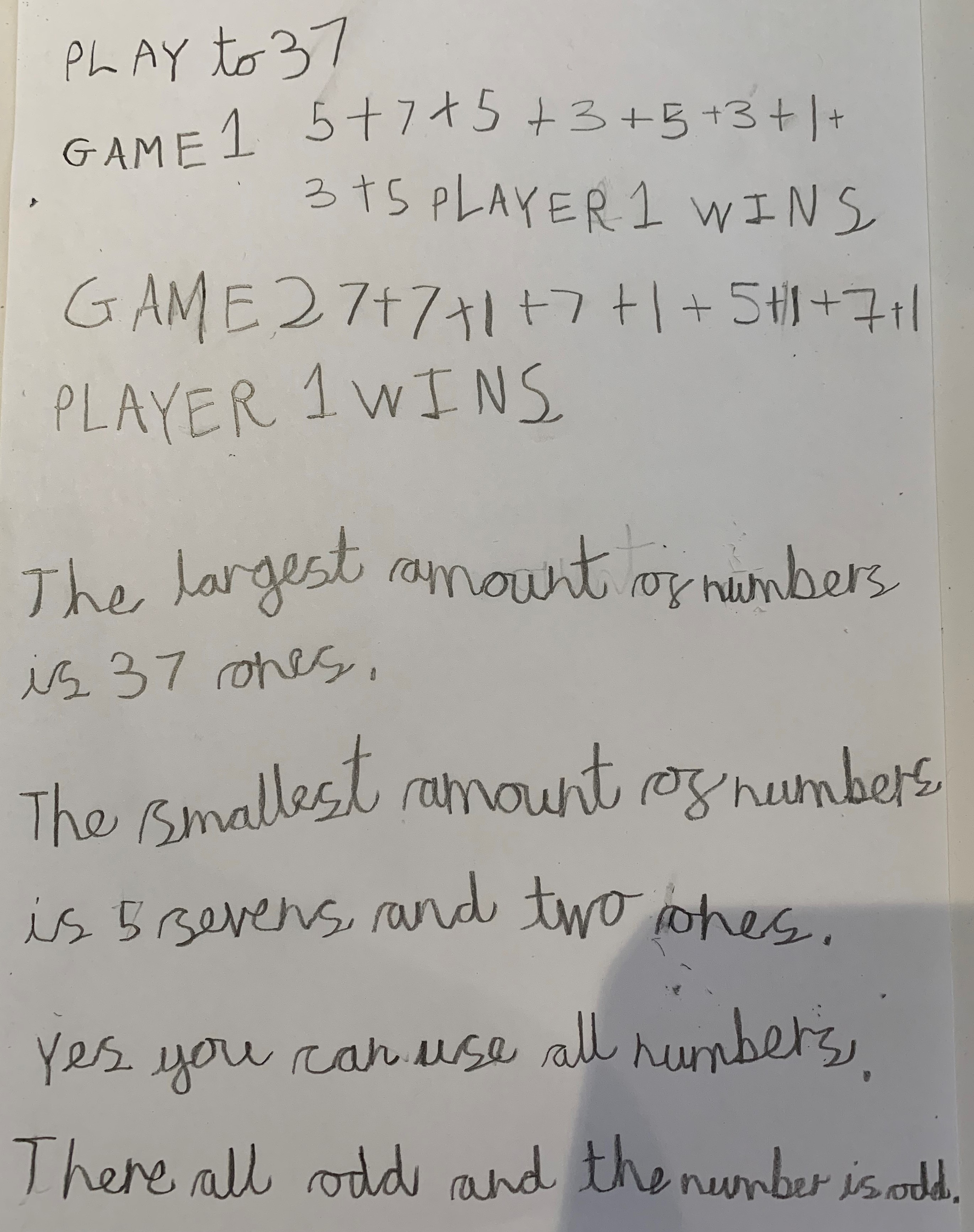
Well done for finding the smallest and largest possible numbers of moves, Ariana! Ariana has worked out that the solution has something to do with the fact that all of the numbers are odd. 

Wren from Pierrepont Gamston Primary School in England sent in this explanation:

Well done Wren, we need to use the fact that two odd numbers makes an even number to work out why Player 1 always wins. 

Ci Hui Minh Ngoc from Kelvin Grove State College in Brisbane, Australia noticed that the total at the end of Player 1's turn will always be odd, while the total on Player 2's turn will always be even. They sent in this explanation:

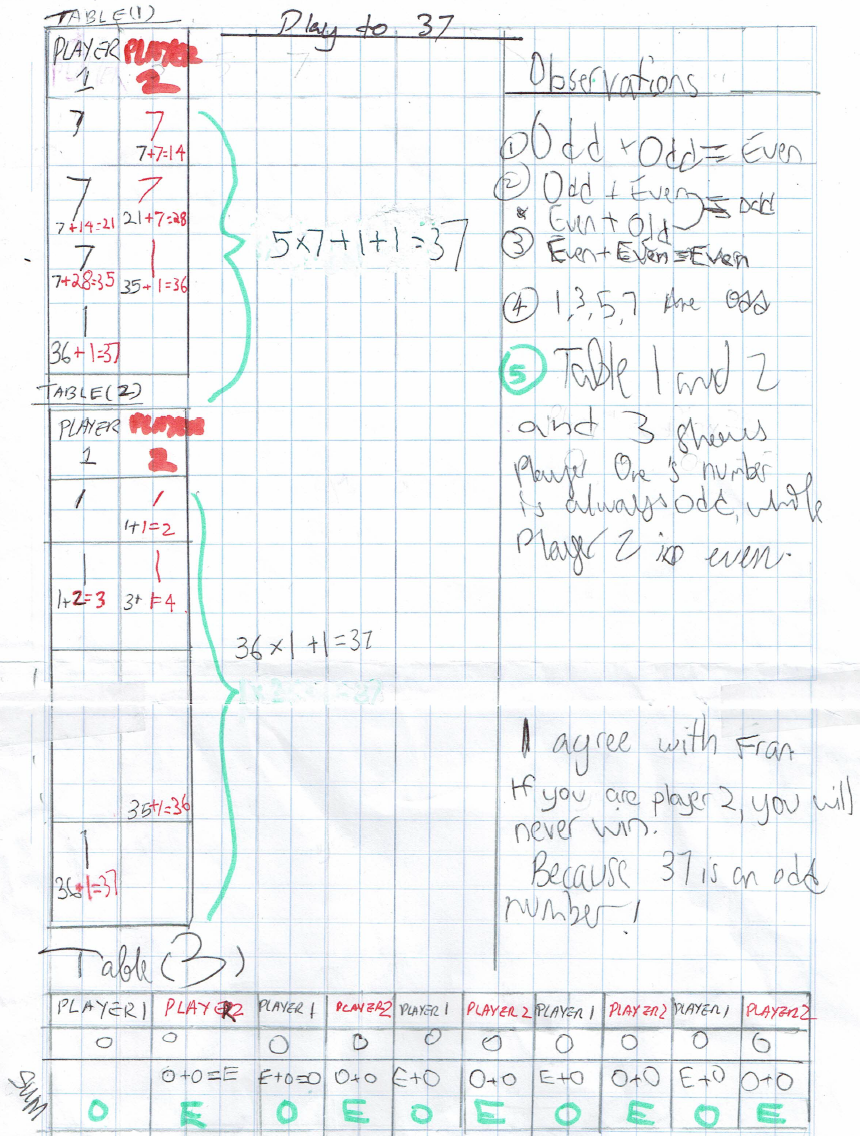
Well done for explaining that, Ci Hui Minh Ngoc - I am now convinced that Player 1 will always win because Player 2 can't get to an odd number on any of their turns.

Ci Hui Minh Ngoc also looked at the different possible numbers of moves. Like Ariana, they found that the lowest number of moves is 7 and the largest is 37. They also found ways of getting to 37 using 9, 13 and 19 moves. I wonder which other numbers of moves are possible between 7 and 37? If you have any ideas about this, please send us an email.