Skip over navigation
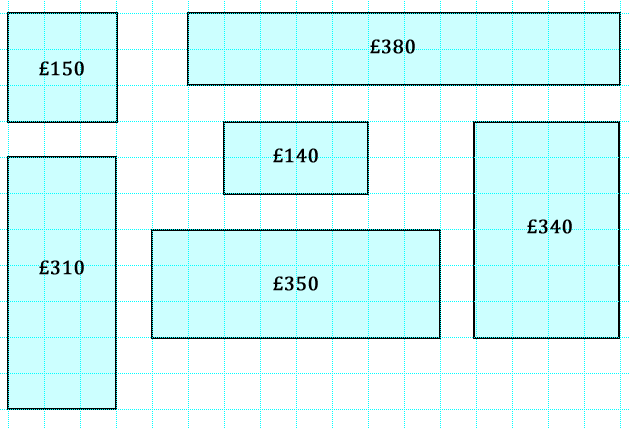
The store in my town which sells windows calculates the price of windows according to the area of glass used and the length of frame needed.
Can you work out how they arrived at the prices of the windows below?
Project the image of the windows and ask the class to suggest what might be important for a store to consider in deciding on the price of their windows. Lead into the task by explaining that the store in your town sets the price of their windows according to the area of glass used and the length of the frame needed.
Give out copies of this sheet, which contains the image, and invite learners to work out (in pairs) how the prices have been calculated. Allow them time to investigate without saying anything more at this stage. As you move round the room, listen out for those children who have useful insights. You may wish to draw everyone back together for a short time to share some of these insights (a mini plenary). This will help those who need encouragement and also gives others chance to articulate their emerging ideas.
Leave time at the end of the lesson to gather everyone together once again to discuss the different ways they approached the problem.
Are there any windows that use the same amount of frame? How do their glass areas differ?
The task Price Match follows on from this one and focuses on creating and using formulae.



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Through the Window
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Through the Window
The store in my town which sells windows calculates the price of windows according to the area of glass used and the length of frame needed.
Can you work out how they arrived at the prices of the windows below?

Why do this problem?
This activity will help children become more familiar with the concepts of area and perimeter as well as giving them lots of practice at calculating both. Rather than being presented with all the necessary information in an immediately accessible way, learners will have to make sense of the activity and decide how to go about tackling it.
Possible approach
Project the image of the windows and ask the class to suggest what might be important for a store to consider in deciding on the price of their windows. Lead into the task by explaining that the store in your town sets the price of their windows according to the area of glass used and the length of the frame needed.Give out copies of this sheet, which contains the image, and invite learners to work out (in pairs) how the prices have been calculated. Allow them time to investigate without saying anything more at this stage. As you move round the room, listen out for those children who have useful insights. You may wish to draw everyone back together for a short time to share some of these insights (a mini plenary). This will help those who need encouragement and also gives others chance to articulate their emerging ideas.
Leave time at the end of the lesson to gather everyone together once again to discuss the different ways they approached the problem.
Key questions
Are there any windows that use the same amount of glass? How do their frame lengths differ?Are there any windows that use the same amount of frame? How do their glass areas differ?
Possible extension
You could encourage learners to create a formula for the total cost of a window, based on the area of glass and its perimeter. The problem Warmsnug Double Glazing is a more challenging version of this problem, which includes a wrongly-priced window.The task Price Match follows on from this one and focuses on creating and using formulae.
Possible support
It may help to suggest that learners write the area and perimeter of each window on the sheet so they don't need to keep re-calculating.You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.
Tiles on a Patio
How many ways can you find of tiling the square patio, using square tiles of different sizes?
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?

