Skip over navigation
In the equation below each square represents a missing digit:
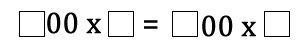
One possible solution is:
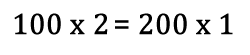
Can you work out some different ways to balance the equation?
This problem provides the children with an opportunity to practise multiplying a single digit number by a multiple of 100. It also reinforces learning about equations being balanced and may lead to conversations about common factors. It encourages children to record their results, notice patterns and make predictions.
Working systematically might involve starting with the lowest values possible. 100 x 1 = 100 x 1. With 100 on each side of the equals sign, can this be made in any other way? Decide as a class if this example actually counts as both sides of the equation are identical. Then move on to 100 x 2 = 200 x 1. Is there another way of making 200? Then try 100 x 3, 100 x 4 and so on.
Alternatively, you might encourage the class to work through all of the options for 100x and then move on to 200 x 1, 200 x 2, 200 x 3 ”¦
Organising results according to how many ways in which the equation can be balanced will support the children to notice patterns and make conjectures.
Some children may move onto the extension tasks (below).
Is there another way of balancing the equation? How many ways are there?
Can you use your knowledge of multiplication facts to help you?
Extension 2: Have a go at Multiply Multiples 3 which involves multiplying a multiple of 10 by another multiple of 10.
Some children may benefit from using Diennes (base 10) apparatus and physically making the amounts. For example, 1200 (12 hundreds) can be organised as 600 x 2, 400 x 3, 300 x 4 and 200 x 6.
Children may be provided with multiplication grids or calculators as appropriate.



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Multiply Multiples 2
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Teachers' Resources
Multiply Multiples 2
In the equation below each square represents a missing digit:
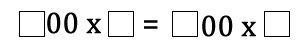
One possible solution is:
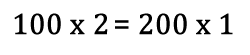
Can you work out some different ways to balance the equation?
Why do this activity?
This problem provides the children with an opportunity to practise multiplying a single digit number by a multiple of 100. It also reinforces learning about equations being balanced and may lead to conversations about common factors. It encourages children to record their results, notice patterns and make predictions.Possible approach
It might be good to let the class explore the problem first before trying to encourage systematic working. The class will hopefully discover issues such as 600 x 1 = 600 x 1 (does this count?!) and 200 x 6 = 300 x 4 = 400 x 3 = 600 x 2 (where there is more than one option). It may be appropriate to then discuss how the class is going to record solutions.Working systematically might involve starting with the lowest values possible. 100 x 1 = 100 x 1. With 100 on each side of the equals sign, can this be made in any other way? Decide as a class if this example actually counts as both sides of the equation are identical. Then move on to 100 x 2 = 200 x 1. Is there another way of making 200? Then try 100 x 3, 100 x 4 and so on.
Alternatively, you might encourage the class to work through all of the options for 100x and then move on to 200 x 1, 200 x 2, 200 x 3 ”¦
Organising results according to how many ways in which the equation can be balanced will support the children to notice patterns and make conjectures.
Some children may move onto the extension tasks (below).
Key questions
Is there another way of balancing the equation? How many ways are there?Can you use your knowledge of multiplication facts to help you?
Possible extensions
Extension 1: Can you explain why there is sometimes just one way of balancing the equation and on other occasions there are lots of ways of doing it? What do you notice about the numbers?Extension 2: Have a go at Multiply Multiples 3 which involves multiplying a multiple of 10 by another multiple of 10.
Possible support
Learners might like to have a go at Multiply Multiples 1 before tackling this activity.Some children may benefit from using Diennes (base 10) apparatus and physically making the amounts. For example, 1200 (12 hundreds) can be organised as 600 x 2, 400 x 3, 300 x 4 and 200 x 6.
Children may be provided with multiplication grids or calculators as appropriate.
You may also like
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?
Bracelets
Investigate the different shaped bracelets you could make from 18 different spherical beads. How do they compare if you use 24 beads?
Sweets in a Box
How many different shaped boxes can you design for 36 sweets in one layer? Can you arrange the sweets so that no sweets of the same colour are next to each other in any direction?

