Skip over navigation
There are three dice, each of them with faces labelled from 1 to 6.
When the dice are rolled they can be combined in six different ways to make a number less than 10 with two decimal places.
For example, if I roll a 2, a 3 and a 6, I can combine them to make 2.36, 2.63, 3.26, 3.62, 6.23 or 6.32.
Now round each of these numbers to the nearest whole number:
2.36 rounds to 2, 2.63 rounds to 3, 3.26 rounds to 3, 3.62 rounds to 4, 6.23 rounds to 6 and 6.32 rounds to 6.
Repeat for other rolls of the dice.
Can each of the six numbers round to the same whole number?
Can each of the six numbers round to a different whole number?
There some interactive dice here that you can use for this problem.
This activity provides a meaningful task for practising rounding decimal numbers to the nearest whole number. It encourages children to record their results, notice patterns and make predictions.
The interactive dice can be used to model the activity on an interactive whiteboard or can be used by the children as they engage with the task. You may also find that individual dice are useful.
As the task is being modelled, the results should be recorded in a table, perhaps like the one below:
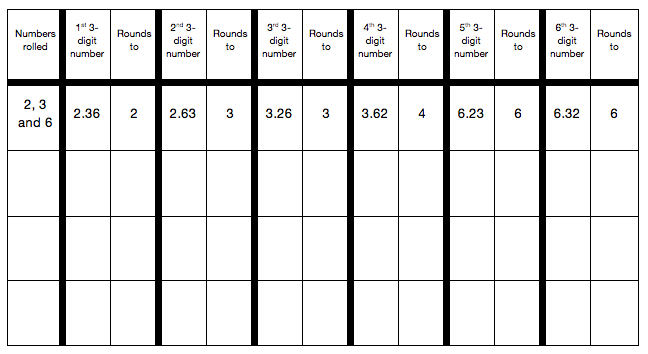
This organisation of results will support the children to notice patterns and conjecture about when numbers will round to different whole numbers.
Some children may move onto the extension tasks (below).
What will they round to? Will they round up or down? Why?
Do they round to the same whole number? Why? When will this happen?
Does it make a difference if the digits rolled are unique?
Extension 2: Did the class find examples where each of the decimal numbers round to a different whole number? Why? Why not?
Extension 3: Having completed the original task, ask the children to add a column to the right hand side of their table to note when numbers round up or down. Can they predict from the initial dice roll, whether the decimal numbers made will round up or down?
Extension 4: What if you change the numbers on the faces of the dice?
Extension 5: What if you round to the nearest tenth?
A number line would also be helpful to support children in reasoning about which whole number is closest to a given decimal number.
Some learners might benefit from having a go at Round the Dice Decimals 1 before tackling this task.
Round the Dice Decimals 2
Age 7 to 11
Challenge Level 
Round the Dice Decimals 2
There are three dice, each of them with faces labelled from 1 to 6.
When the dice are rolled they can be combined in six different ways to make a number less than 10 with two decimal places.
For example, if I roll a 2, a 3 and a 6, I can combine them to make 2.36, 2.63, 3.26, 3.62, 6.23 or 6.32.
Now round each of these numbers to the nearest whole number:
2.36 rounds to 2, 2.63 rounds to 3, 3.26 rounds to 3, 3.62 rounds to 4, 6.23 rounds to 6 and 6.32 rounds to 6.
Repeat for other rolls of the dice.
Can each of the six numbers round to the same whole number?
Can each of the six numbers round to a different whole number?
There some interactive dice here that you can use for this problem.
Why do this activity?
This activity provides a meaningful task for practising rounding decimal numbers to the nearest whole number. It encourages children to record their results, notice patterns and make predictions.Possible approach
A possible starting point is using a number line to remind the class what is meant by rounding.The interactive dice can be used to model the activity on an interactive whiteboard or can be used by the children as they engage with the task. You may also find that individual dice are useful.
As the task is being modelled, the results should be recorded in a table, perhaps like the one below:
This organisation of results will support the children to notice patterns and conjecture about when numbers will round to different whole numbers.
Some children may move onto the extension tasks (below).
Key questions
Which numbers can we make?What will they round to? Will they round up or down? Why?
Do they round to the same whole number? Why? When will this happen?
Does it make a difference if the digits rolled are unique?
Possible extensions
Extension 1: Did the class find examples where some of the decimal numbers round to the same whole number? Can they then come up with a rule about when this will happen? When will two round to the same? Or three? Or four? Or five? Or all six?Extension 2: Did the class find examples where each of the decimal numbers round to a different whole number? Why? Why not?
Extension 3: Having completed the original task, ask the children to add a column to the right hand side of their table to note when numbers round up or down. Can they predict from the initial dice roll, whether the decimal numbers made will round up or down?
Extension 4: What if you change the numbers on the faces of the dice?
Extension 5: What if you round to the nearest tenth?
Possible support
Copies of the table to write straight into would be useful.A number line would also be helpful to support children in reasoning about which whole number is closest to a given decimal number.
Some learners might benefit from having a go at Round the Dice Decimals 1 before tackling this task.
You may also like
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?
Bracelets
Investigate the different shaped bracelets you could make from 18 different spherical beads. How do they compare if you use 24 beads?
Sweets in a Box
How many different shaped boxes can you design for 36 sweets in one layer? Can you arrange the sweets so that no sweets of the same colour are next to each other in any direction?