Skip over navigation
Three Triangles
Age 7 to 11
Challenge Level 
Three Triangles
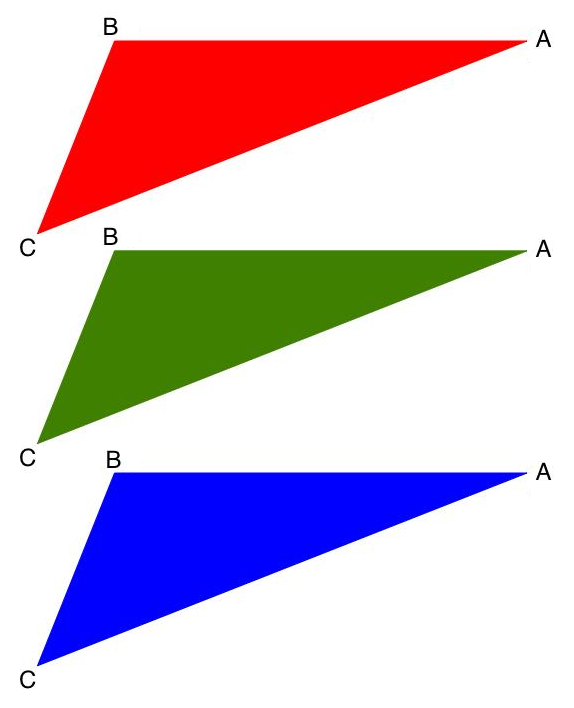
We start with three triangles the same size and shape. I've coloured them differently but that's not important. I've labelled each corner for you.
Using three pieces of thick paper or card on top of each other, carefully cut out a triangle shape so that you have three identical triangles.
Look how I've started to put the different corners together:
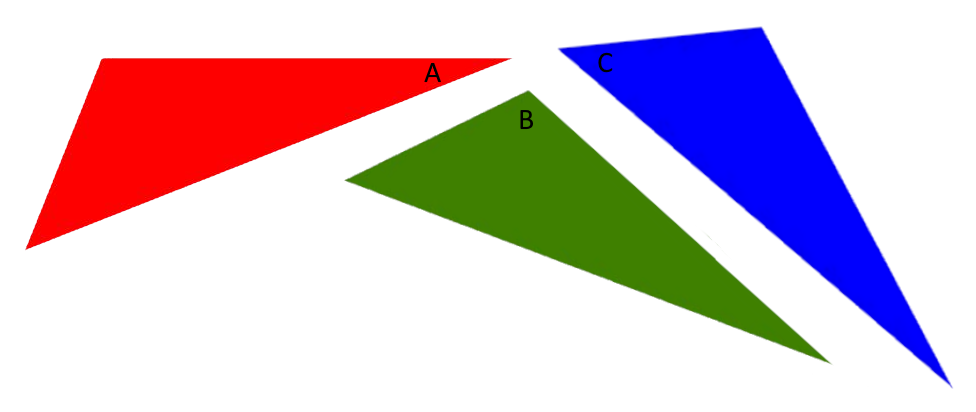
Put your corners together completely so that they close up and have no gaps or overlapping.
Try it again with a new set of three triangles.
You could try it many times with very different triangles.
What can you say about it?
What if you use two sets of three triangles together?
Look how I've started to put the different corners together:
Put your corners together completely so that they close up and have no gaps or overlapping.
Try it again with a new set of three triangles.
You could try it many times with very different triangles.
What can you say about it?
What if you use two sets of three triangles together?
Why do this problem?
This problem encourages pupils to explore angular properties of triangles. It leads into predicting what properties all triangles have in common.
Possible approach
Invite learners to tell you what they know about triangles. Use what they say to lead into the task: provide each pupil or pairs or pupils with three pieces of suitable stiff paper or card, a ruler, pencil and scissors and ask them to cut out three identical triangles.
Then, together as a group, explore putting the triangles together including the way suggested in the challenge.
Lead a discussion about what they notice and encourage any further ideas for exploration.
Lead a discussion about what they notice and encourage any further ideas for exploration.
Key questions
Tell me about what's happened (when the three triangles are put together as in the challenge).
Have you tried other sets of three triangles?
What else could you explore?
Have you tried other sets of three triangles?
What else could you explore?
