Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
What Could It Be?



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
What Could It Be?
What Could It Be? printable sheet
In the calculation below, the box represents a missing digit:
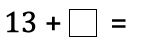
What could go in the box? What would the total be each time?
Which is the highest/lowest total?
Which totals are odd/even?
Why do this activity?
This activity provides an opportunity for children to practise their addition skills through a meaningful open-ended task. It encourages children to record their results, notice patterns and make predictions.
Possible approach
A possible starting point is to begin with a question such as 3+__= and ask the class to come up with what it could be. The box represents one missing digit. The children should be encouraged to come up with as many answers as possible. How will you know when you've found them all? As the possibilities are collated, these could be organised systematically so that the children notice the
pattern:
3 + 0 = 3
3 + 1 = 4
3 + 2 = 5
3 + 3 = 6 and so on.
It is possible to draw out which totals are odd/even, which is the highest/lowest total, which totals are single digit numbers and so on.
Children can then be set a similar challenge working within 20 or could move on to the original problem. Some children may start with or move onto the extension tasks (below).
Key questions
Which numbers have you added?
What totals were possible?
Which is the highest/lowest total?
Which totals are odd/even? Could you have predicted this?
Are there different ways of getting to the same total?
Possible extensions
Extension 1:
1__ + 1__ = This time there are two boxes and each represents a missing digit.
What could go in the box? What if the missing digits are the same, what if they are different? What would the total be each time? Which is the highest/lowest total?
Can you find two different ways of getting the same total but using different digits?
Extension 2:
Make up your own similar problem.
Possible support
Whatever resources are being used to support the development of addition skills are appropriate to use for this challenge. For example: a 100 square, a number line or track, a bead string, Diennes (base 10) apparatus, etc.
Related Collections
You may also like
Biscuit Decorations
Andrew decorated 20 biscuits to take to a party. He lined them up and put icing on every second biscuit and different decorations on other biscuits. How many biscuits weren't decorated?

