Unit Differences
Unit Differences
Unit Differences printable sheet
This challenge is about finding the difference between numbers which have the same tens digit.
Here are two examples where I've decided to use numbers which have two tens:
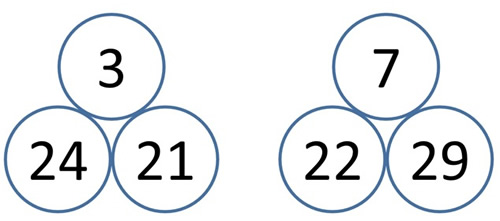
The number above is always the difference between the two beneath it.
Can you find different pairs of numbers with a difference of 1 or 2 or 3 or 4 ... and so on?
Can you find more than one way of doing it?
Why do this activity?
This activity provides a context for practising finding a small difference between two two-digit numbers. It encourages children to record their results, notice patterns and make predictions.
Possible approach
The children may need reminding about what it means to find the difference between numbers, and some strategies for doing this.
A possible starting point for the activity is using the same idea but with single digit numbers, perhaps starting with 7 and 9 on the bottom first. This is an opportunity to model how to find the difference and also how to write this difference into the circle on top.
As a class, you could explore other possibilities for having a difference of 2 starting with just single-digit numbers (1 and 3, 2 and 4) and as you collect the results in, they could be organised to enable the children to notice the patterns.
As children attempt the main task, they may explore different ways of having a difference of 5 (for example) within the twenties (21 and 26, 22 and 27) or across different tens (21 and 26, 31 and 36, 43 and 48). Encourage the children to record their work and spot patterns as in the introduction. This sheet of blank pyramids
may be useful.
Some children may move onto the extension task (below).
Key questions
What is the difference between the numbers?
Do any other pairs of numbers have the same difference?
Can you spot a pattern?
Possible extensions
Extension 1: This time there are three numbers at the bottom of the pyramid (all with the same number of tens) but otherwise the pyramid is constructed in exactly the same way.
3 is the difference between 24 and 21.
5 is the difference between 21 and 26.
2 is the difference between 3 and 5.
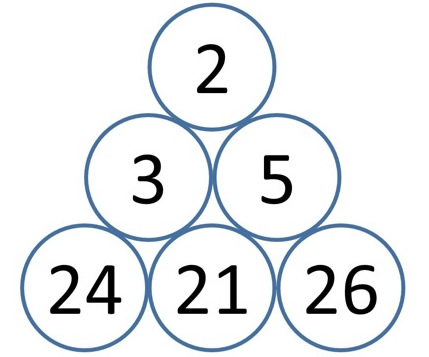
Children could make some pyramids of their own. Here is a sheet of blank 'three tiered' pyramids.
Extension 2: Can learners find different pyramids with the same number at the top?
Possible support
A 100 square or number line/track.
Blank pyramids.
You may also like
Let's Investigate Triangles
Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?
