Five Steps to 50

Year 4 from Tidcombe Primary School sent in the following:

Abbie, Olive, Edith and Piran all noticed the diagonal pattern when they plotted the numbers that worked on a hundred square. They also noticed that something slightly changed the pattern in the middle. Daisy noticed that the numbers in the 2s column worked if they had an even number of tens but 2 didn't work because it was too far away from 50. Olive noticed that this pattern changed from column to column, for example in the 1s column, only the numbers with an odd number of tens worked. Fleur noticed that: when you find a number that you can get to 50 in 5 steps, if you subtract that number from 100, then you get another number that you can get to 50 in 5 steps.



Here is a solution which is based on a similar idea.  This pupil also used a hundred square to very effectively represent which numbers he could, and could not, reach when taking five steps to fifty.  In the image below, 

Black = Works and can be rolled with a 1-6 die

Blue = Works and can't be rolled with a 1-6 die

Red = Doesn't work

 

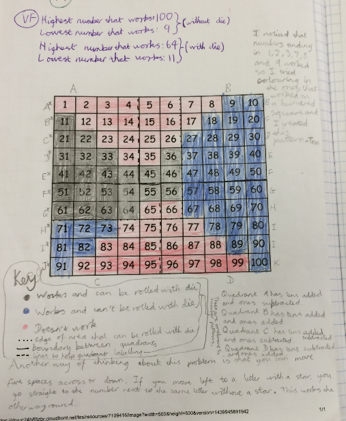
He says:

Another way of thinking about this problem is that you can move five spaces across or down.

Can you follow his reasoning?