Rhombuses from Diagonals

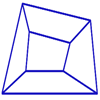
Abbie from Malet Lambert school thought about the best way to set out this problem:

When creating as many rhombuses as you can, I believe that you should draw
all your diagonals out at once that are going to be in the centre of your
rhombuses. This then means that you ca just set your mind on the lines
surrounding them, so you can find as many rhombuses as you can.

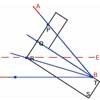
Chris tried making lots of rhombuses from one diagonal:

I thought that the answer was infinite from the start, because there are no
restrictions on how large the shape can be. There are no restrictions on
how large a plane can be or how far it can go on for.

To test this out I started with a diagonal which was $1$ unit across, it
seemed the most logical place to start. I drew a shape resembling a square
which had had two of it's corners drawn out, one unit in a perpendicular
direction to the original diagonal that I had drawn, as you can see below.I
then drew another shape identical to the first with its two "drawn out
corners". This time however, I extended the shape two units in each
direction.I continued to do this. I then drew the conclusion that you could
continue to do this forever, with no limitation.

Here is a picture of the rhombuses that Chris drew.