Skip over navigation
Areas of Squares
Noah from Bligh Junior School in the UK did some experimenting.
I can put it inside of a bigger square which has all the four vertices of the initial square on its sides and has only vertical and horizontal sides. I notice that the corner triangles form the initial square if rearranged. Therefore the area of the big square equals twice the area of the initial square. We can easily compute the area of the big square by counting the unit squares on one side and square the result. By dividing this result by two, we get the area of the square.
He also found a method for more general tilts:
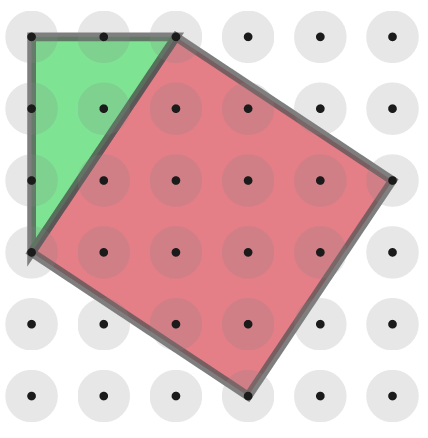
Draw a larger square around the tilted square so that the vertices of the tilted square touch the edges of the larger square. The larger square is drawn straight i.e. using vertical and horizontal lines as sides. This creates 4 right angled triangles in the space between the squares.
Find the area of a right angled triangle, multiply it by 4 then deduct it from the area of the larger square. Your answer will be the area of the tilted square
Katie from Sacred Heart Catholic College in the UK approached the problem differently and wrote a very clear solution.
1. Chose one side of your square, draw two more lines to create a right
angle triangle with one vertical and one horizontal cathetus.
2. Count the spaces of the two sides you have drawn.
3. Then, using pythagoras's rule, square each number and add the two
together.
4. The sum of these numbers then needs to be square rooted.
5. And thats how long each side of the square is.
6. After this we need to find the area.
7. So we times the two sides of the square together, and you have your
answer.
Hannah and Matthew, also from Sacred Heart Catholic College and Caistor Yarborough Academy Maths Club, all in the UK, had similar ideas to Katie.
Once you have your right angled triangle, you square the two shorter sides to find the length of the hypotenuse, using Pythagoras' rule which says $a^2+b^2=c^2$. However, what we are interested in is the area of a square with sides of length $c$, and this area would be $c^2$. So we know that
$$\text{area of the square } =a^2+b^2$$
where $a$ and $b$ are the sides of the right angled triangle which we drew.
Well done to everyone who sent in a solution.
I can put it inside of a bigger square which has all the four vertices of the initial square on its sides and has only vertical and horizontal sides. I notice that the corner triangles form the initial square if rearranged. Therefore the area of the big square equals twice the area of the initial square. We can easily compute the area of the big square by counting the unit squares on one side and square the result. By dividing this result by two, we get the area of the square.
He also found a method for more general tilts:
Draw a larger square around the tilted square so that the vertices of the tilted square touch the edges of the larger square. The larger square is drawn straight i.e. using vertical and horizontal lines as sides. This creates 4 right angled triangles in the space between the squares.
Find the area of a right angled triangle, multiply it by 4 then deduct it from the area of the larger square. Your answer will be the area of the tilted square
Katie from Sacred Heart Catholic College in the UK approached the problem differently and wrote a very clear solution.
1. Chose one side of your square, draw two more lines to create a right
angle triangle with one vertical and one horizontal cathetus.
2. Count the spaces of the two sides you have drawn.
3. Then, using pythagoras's rule, square each number and add the two
together.
4. The sum of these numbers then needs to be square rooted.
5. And thats how long each side of the square is.
6. After this we need to find the area.
7. So we times the two sides of the square together, and you have your
answer.
Hannah and Matthew, also from Sacred Heart Catholic College and Caistor Yarborough Academy Maths Club, all in the UK, had similar ideas to Katie.
Once you have your right angled triangle, you square the two shorter sides to find the length of the hypotenuse, using Pythagoras' rule which says $a^2+b^2=c^2$. However, what we are interested in is the area of a square with sides of length $c$, and this area would be $c^2$. So we know that
$$\text{area of the square } =a^2+b^2$$
where $a$ and $b$ are the sides of the right angled triangle which we drew.
Well done to everyone who sent in a solution.
You may also like
Pair Sums
Five numbers added together in pairs produce: 0, 2, 4, 4, 6, 8, 9, 11, 13, 15 What are the five numbers?
Summing Consecutive Numbers
15 = 7 + 8 and 10 = 1 + 2 + 3 + 4. Can you say which numbers can be expressed as the sum of two or more consecutive integers?
Big Powers
Three people chose this as a favourite problem. It is the sort of problem that needs thinking time - but once the connection is made it gives access to many similar ideas.