Spirals, Spirals
Spirals, Spirals
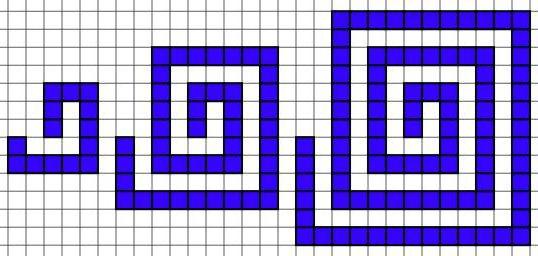
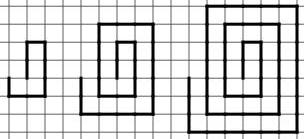
The first (on the left) uses the little squares to make the spiral, the second (on the right) uses the sides of the little squares to build the spiral.
I gave myself some rules (often a good idea!):
1/ There is a space throughout making them a kind of "open" spiral.
2/ I finished each spiral in line with where it started in the middle.
3/ I made a number of spirals each one having one more "circuit" (going around) than the previous one.
So these would not do as they don't obey all the rules:
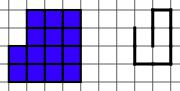
I then started exploring things like the number of little squares/lines in my group of spirals.
So now is the time for you for you to explore your growing spirals.
What do you notice?
Why do this problem?
This activity was initially developed for Wild Maths, our sister site, to encourage learners to be creative mathematicians. Mathematics is certainly a creative subject. It involves spotting patterns, making connections, finding new ways of looking at things and using what you already know in new contexts. Creative mathematicians play around with
examples, draw pictures, have the courage to experiment and ask good questions. (Wild Maths is aimed at individual learners, rather than teachers so the notes below only appear on NRICH.)
Possible approach
It would be good to either have a big white board displaying the first spiral or a large physical one that all pupils can see. You could use cubes on the same unit sized squared paper, and you could demonstrate the start of a spiral. You could then have pupils continuing on the demonstration checking for obeying the rules.When you think they've got the idea as to how each spiral "grows" then they could explore by making larger and larger spirals. You could encourage learners to explore the "squares" spiral as much as possible before moving on to the "lines" spiral. Alternatively, you could split the group up so that half explores one type of spiral and the other half explores the other spiral.
Key questions
Tell me about your spiral.
What counting have you decided to do?
Have you noticed anything?
What will you do next?
Possible extension
If the pupils can think for themselves of an idea to extend the exploration by changing one of the rules slightly, that would be good. If not you could introduce the idea of exploring a "squares" spiral of the same number of circuits but changing the number of squares that follow the first square. (So instead of there being two more squares going up you could have three and then four etc.)
Possible support
Some pupils may need help moving from the practical to recording. Some may have difficulty counting accurately.
You may also like
Counting Counters
Take a counter and surround it by a ring of other counters that MUST touch two others. How many are needed?
Cuisenaire Squares
These squares have been made from Cuisenaire rods. Can you describe the pattern? What would the next square look like?
Doplication
We can arrange dots in a similar way to the 5 on a dice and they usually sit quite well into a rectangular shape. How many altogether in this 3 by 5? What happens for other sizes?