Mega Quadratic Equations

Why do this problem?

Routine exercises often give students the impression that it is easy to spot the appropriate technique to solve problems in mathematics. The equations in this problem require students to make connections between different areas of mathematics, namely quadratic equations and indices, and to use what they know to solve a problem which at first glance looks much harder than it is.

Possible approach

Display the equation:
$$(x^2 - 5x + 5)^{(x^2 - 11x + 30)} = 1$$
"Can you find at least one solution to this equation?"
Give students some time to work on their own or with a partner. As they are working, listen out for different approaches: some students may start with the realisation that raising something to the power zero is $1$, or that raising $1$ to any power is $1$.

After a while, invite a couple of students out to the board to share their solutions. Then reveal that the equation has six solutions in total, and challenge them to use what they have learned to find the remaining solutions.

Then share the next equation: $(x^2 - 7x + 11)^{(x^2 - 13x + 42)} = 1$
Once students have found all solutions, they may wish to explore other equations in the same family, and there are also some suggestions for Mega Quadratic Equations which have fewer than six solutions.

Key questions

Do you know any solutions to the equation $a^b=1$?
How can each solution to $a^b=1$ help you to find solutions to the equations?

Possible support

Students may be put off by the apparent complexity of this task, so reassure them that all they need to be able to do is solve quadratic equations and know their index laws! The hint "Do you know any solutions to the equation $a^b=1$?" may help them to find a fruitful line of enquiry.

Possible extension

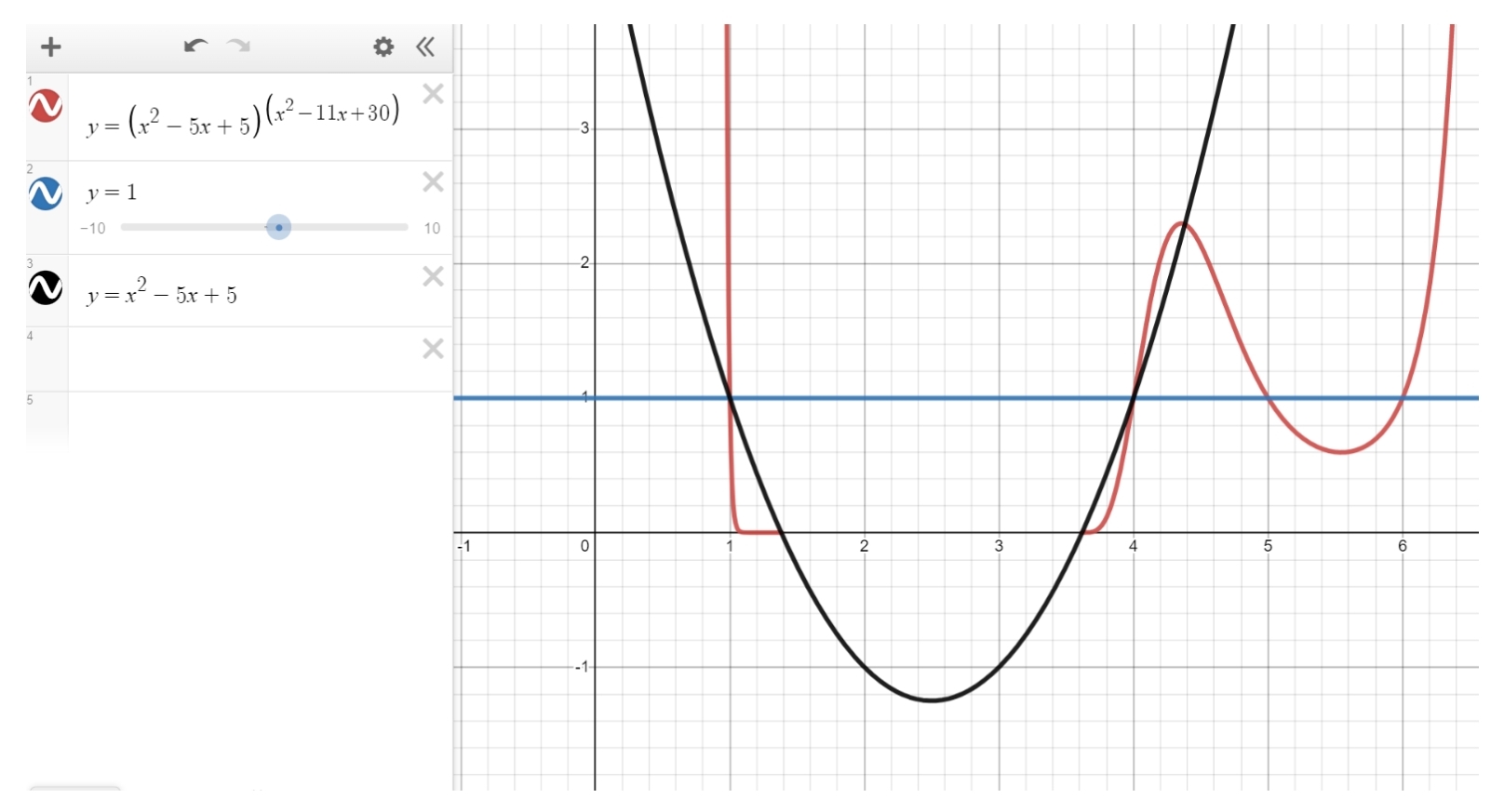
Invite students to plot the equations using graphing software such as Desmos. There are some interesting features to explain; in particular, not all six solutions show up graphically without resorting to complex number plots!

The picture below shows the first equation, and also graphs the base of the equation $(y=x^2 - 5x - 5)$.  From this it can be seen that Desmos has difficulties graphing $y=(x^2 - 5x + 5)^{(x^2 - 11x + 30)}$ when the base is negative.

Here is a link to the Desmos Graphs.