Making a Difference

Making a Difference printable worksheet
 

There are a number of ways the digits $2, 5, 7, 8$ can be placed in a subtraction sum like the one below:





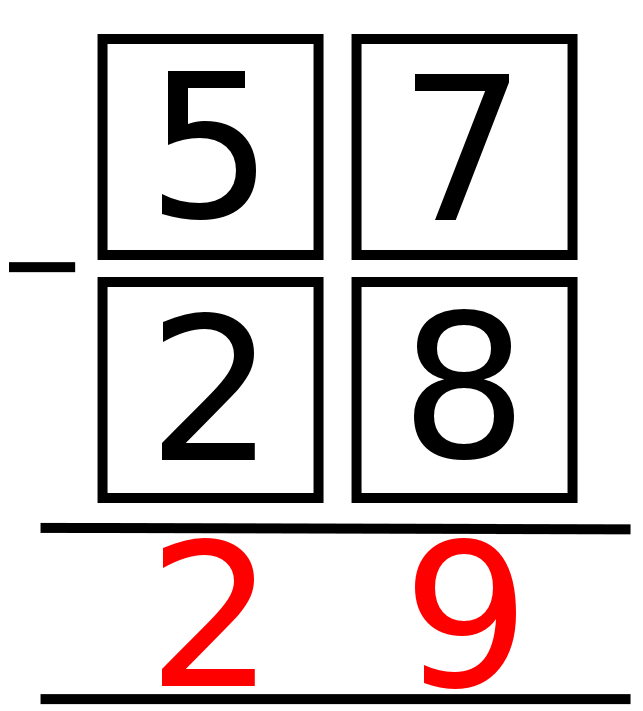
In this example, the answer is 29.

Can you rearrange the four digits to find all the (positive) answers it is possible to make?

 



Here are two follow-up questions you might like to consider:

• Can you work out which four digits you need to start with to be able to get all the possible answers $7, 9, 11, 13, 18, 22, 29$ and $31$?
   
• Can you show that, if we're only allowed to use consecutive digits (e.g. $5, 6, 7, 8$), $31$ is the largest possible answer and $7$ is the smallest?

With thanks to Don Steward, whose ideas formed the basis of this problem.