Quadrilaterals in a Square

Quadrilaterals in a Square printable sheet
Quadrilaterals in a Square downloadable slides

Suppose we have a yellow square of side length $a+b$.

We can draw quadrilaterals in this square so that one vertex lies on each side of the square, and cuts each side into one segment of length $a$ and one segment of length $b$, as below:

 

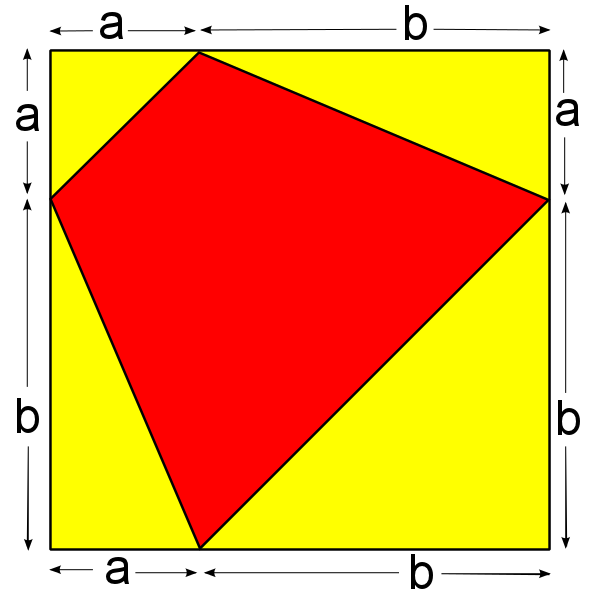
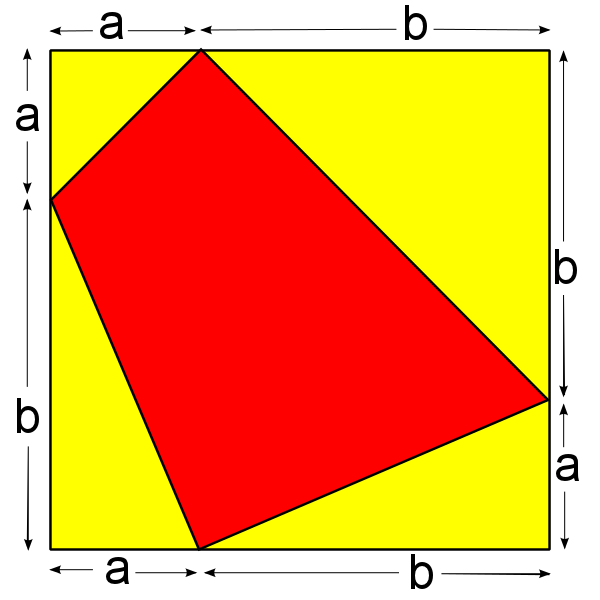
Can you prove that in each of these images the area of the red quadrilateral is exactly half the area of the yellow square?

Try to find two different ways to prove it - one algebraic, and one geometric.


Here are two more images showing quadrilaterals drawn on the yellow square.

            

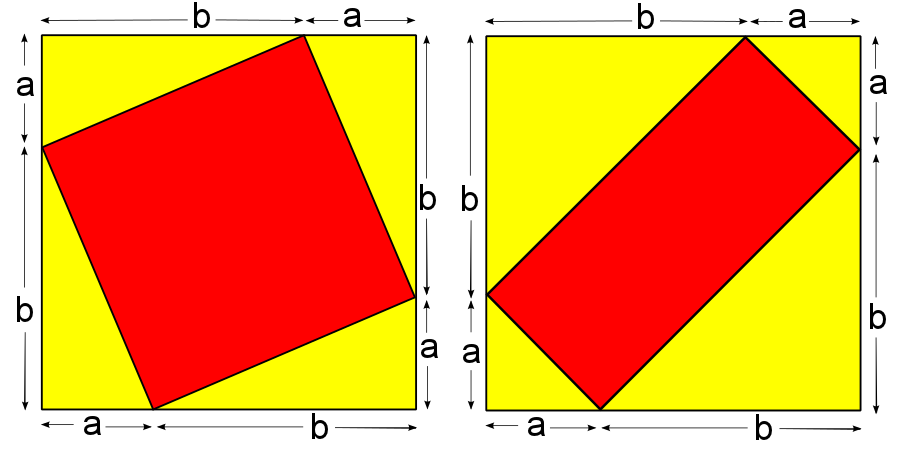
Can you prove that the areas of these two red quadrilaterals sum to the area of the yellow square?

Again, try to prove this in both an algebraic and a geometric way.

With thanks to Don Steward, whose ideas formed the basis of this problem.