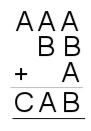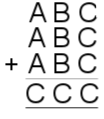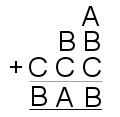Cryptarithms
Cryptarithms printable worksheet
A cryptarithm is a mathematical puzzle where the digits in a sum have been replaced by letters.
In each of the puzzles below, each letter stands for a different digit.
Bearing in mind that none of the numbers below have 0 as a leading digit, can you find a solution to all of these cryptharithms?
Do any of them have more than one solution?
| 1. |
 |
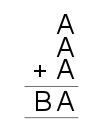2. |
 |
3. |
 |
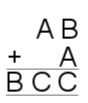4. |
 |
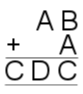| 5. |
 |
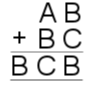6. |
 |
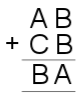7. |
 |
8. |
 |
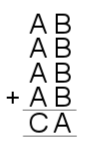| 9. |
 |
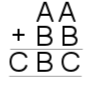10. |
 |
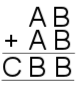11. |
|
12. |
 |
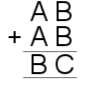| 13. |
|
14. |
 |
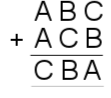15. |
 |
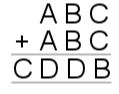16. |
 |
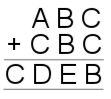| 17. |
|
18. |
 |
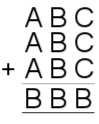19. |
 |
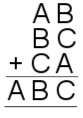20. |
|
| 21. |
 |
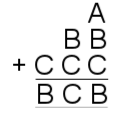22. |
 |
23. |
|
Final Challenge
Is it possible for all of the digits 1 to 9 to appear exactly once in the addition below?
+ # # #
# # #
Using each digit from 1 to 9 once, what is the largest sum you can obtain in the addition above?
If you enjoyed this problem, you may also like to take a look at Two and Two.
With thanks to Don Steward, whose ideas formed the basis of this problem.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Adding All Nine
Make a set of numbers that use all the digits from 1 to 9, once and once only. Add them up. The result is divisible by 9. Add each of the digits in the new number. What is their sum? Now try some other possibilities for yourself!