Skip over navigation
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Mixing Lemonade Poster
Age 11 to 14
Challenge Level 





- Problem
- Student Solutions
Answer: the first glass tasted stronger
How do you know?
Method 1: making the same amount of lemon juice

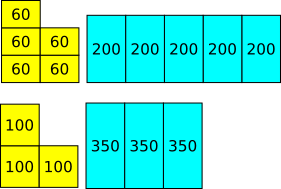
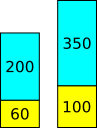
First glass lemon:water 60:200
Second glass lemon:water 100:350
60$\times$5 = 100$\times$3 = 300
200$\times$5 = 1000, so first glass lemon:water 300:1000
350$\times$3 = 1050, so second glass lemon:water 300:1050
First glass has less water for the same amount of lemon juice so the first glass tastes stronger.
Method 2: making the same amount of water

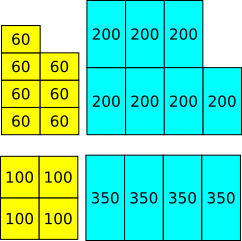
First glass lemon:water 60:200
Second glass lemon:water 100:350
200$\times$7 = 350$\times$4 = 1400
60$\times$7 = 420, so first glass lemon:water 420:1400
100$\times$4 = 400, so second glass lemon:water 400:1400
First glass has more lemon juice for the same amount of water so the first glass tastes stronger.
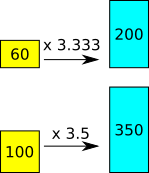
Method 3: scaling lemon juice to water

First glass: scale factor from lemon juice to water is 3.333
Second glass: scale factor from lemon juice to water is 3.5
There is more water compared to lemon juice in the second glass, so the first glass tastes stronger.
Method 4: fractions

First glass: $\frac{60}{260} =\frac6{26} = \frac3{13}$ lemon juice
Second glass: $\frac{100}{450} = \frac{10}{45} = \frac29$ lemon juice
Common denominator: $13\times9$
First glass: $\frac3{13} = \frac{27}{13\times9}$
Second glass: $\frac27 = \frac{26}{13\times9}$
The first glass has a greater fraction of lemon juice so it tastes stronger.

