Skip over navigation
Can You Find ... Asymptote Edition
Age 16 to 18
Challenge Level 
Aneesh from West Island School Hong Kong, Louis from EMS, and Emily from Doctor Challoner's High School submitted solutions to this problem.
Aneesh first found that $\frac{x^3-4x}{x^2-1}$ produced a graph of this shape, and then generalised his findings:
Functions of the form $\frac{(x)(x+a)(x-a)}{(x+b)(x-b)}$ where $a>b$ seem to obey the general shape of the displayed graph.
In order to work this out, I first considered the asymptotes on the graph. The function seemed to have two vertical asymptotes, evenly spaced from $0$ which I originally thought were at $x=1$ and $x=-1$. So I knew that the denominator of my rational function should have roots at 1 and -1.
Furthermore I considered the limits as $x$ approached $0$,$1$,$-1$ and infinity of the function shown. I knew that the limit as $x$ approached positive infinity of the function was an oblique asymptote (that looked like the line $y=x$).
The limit as x approached $1$ from the right hand side was negative infinity, and so I knew that the numerator must be negative for $x$ close to but greater than $1$.
By symmetry, I knew that my numerator must be positive for $x$ close to but less than $-1$ from the LHS.
Keeping this in mind, I then considered the roots of my function. They were $0$, a number greater than $1$ (greater than my positive vertical asymptote) and a number less than $-1$, (less than my negative vertical asymptote). So the roots of my numerator were $0$, $2$, $-2$. So I initially wrote down $x(x+2)(x-2)$ for my numerator. This numerator even satisfied my previously imposed conditions, because if I pick an $x$ value close to but greater than $1$, I will get a negative value on my numerator. And if I pick an x value close to but less than $-1$, I will get a poitive value in my numerator. This is because $(x-2)(x)$ would always yield negative, the product of two negative numbers is a positive.
So in general, the form of such a function would be $\frac{(x)(x+a)(x-a)}{(x+b)(x-b)}$. Moreover, on taking the limit to negative or positive infinity of the expression chosen above, as the numerator is a polynomial of degree one greater than the polynomial below, the function gets closer and closer to $\frac{x^3}{x^2} = x$. Which yields the oblique asymptote.
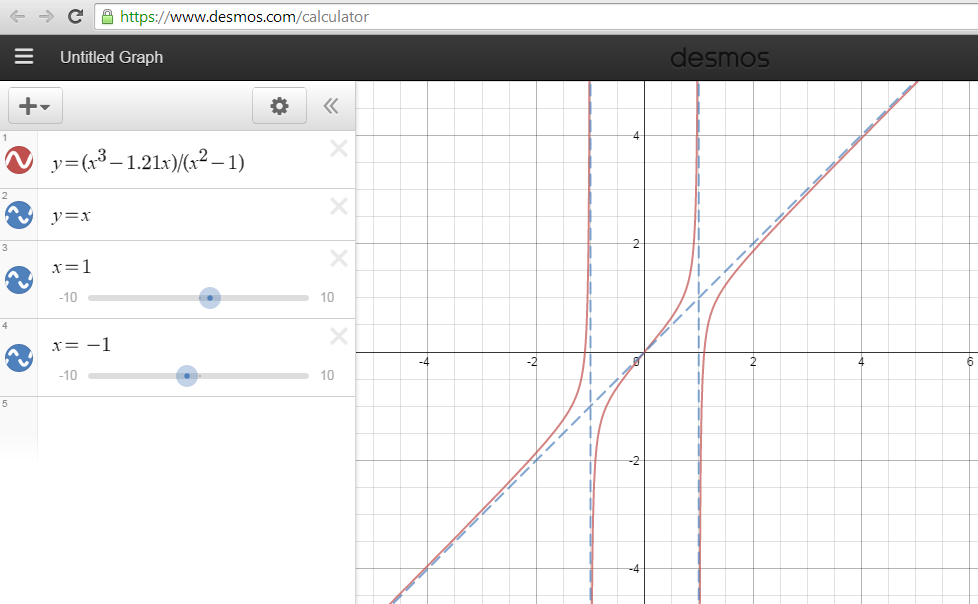
Louis thought similarly about general polynomial functions which produce this graph, and decided on the function $\frac{x^3-1.21}{x^2-1}$. Below is a picture of his graph in Desmos:
Emily also thought about general polynomial functions which produce graphs of this shape, and went on to think about whether it was possible to produce this graph using trigonometric functions. Here is a link to her solution.
Thank you everybody!
Aneesh first found that $\frac{x^3-4x}{x^2-1}$ produced a graph of this shape, and then generalised his findings:
Functions of the form $\frac{(x)(x+a)(x-a)}{(x+b)(x-b)}$ where $a>b$ seem to obey the general shape of the displayed graph.
In order to work this out, I first considered the asymptotes on the graph. The function seemed to have two vertical asymptotes, evenly spaced from $0$ which I originally thought were at $x=1$ and $x=-1$. So I knew that the denominator of my rational function should have roots at 1 and -1.
Furthermore I considered the limits as $x$ approached $0$,$1$,$-1$ and infinity of the function shown. I knew that the limit as $x$ approached positive infinity of the function was an oblique asymptote (that looked like the line $y=x$).
The limit as x approached $1$ from the right hand side was negative infinity, and so I knew that the numerator must be negative for $x$ close to but greater than $1$.
By symmetry, I knew that my numerator must be positive for $x$ close to but less than $-1$ from the LHS.
Keeping this in mind, I then considered the roots of my function. They were $0$, a number greater than $1$ (greater than my positive vertical asymptote) and a number less than $-1$, (less than my negative vertical asymptote). So the roots of my numerator were $0$, $2$, $-2$. So I initially wrote down $x(x+2)(x-2)$ for my numerator. This numerator even satisfied my previously imposed conditions, because if I pick an $x$ value close to but greater than $1$, I will get a negative value on my numerator. And if I pick an x value close to but less than $-1$, I will get a poitive value in my numerator. This is because $(x-2)(x)$ would always yield negative, the product of two negative numbers is a positive.
So in general, the form of such a function would be $\frac{(x)(x+a)(x-a)}{(x+b)(x-b)}$. Moreover, on taking the limit to negative or positive infinity of the expression chosen above, as the numerator is a polynomial of degree one greater than the polynomial below, the function gets closer and closer to $\frac{x^3}{x^2} = x$. Which yields the oblique asymptote.
Louis thought similarly about general polynomial functions which produce this graph, and decided on the function $\frac{x^3-1.21}{x^2-1}$. Below is a picture of his graph in Desmos:
Emily also thought about general polynomial functions which produce graphs of this shape, and went on to think about whether it was possible to produce this graph using trigonometric functions. Here is a link to her solution.
Thank you everybody!
You may also like
Powerful Quadratics
This comes in two parts, with the first being less fiendish than the second. It’s great for practising both quadratics and laws of indices, and you can get a lot from making sure that you find all the solutions. For a real challenge (requiring a bit more knowledge), you could consider finding the complex solutions.
Discriminating
You're invited to decide whether statements about the number of solutions of a quadratic equation are always, sometimes or never true.
Factorisable Quadratics
This will encourage you to think about whether all quadratics can be factorised and to develop a better understanding of the effect that changing the coefficients has on the factorised form.