Star Polygons
Here is a five-pointed star:
Draw a couple of five pointed stars of your own, making sure your lines are nice and straight!
Measure the interior angles at the five points and add them together.
What do you notice?
You may find this set of slides from Karen Hancock useful - they show how you can use the Desmos geometry construction tools to tackle this problem.
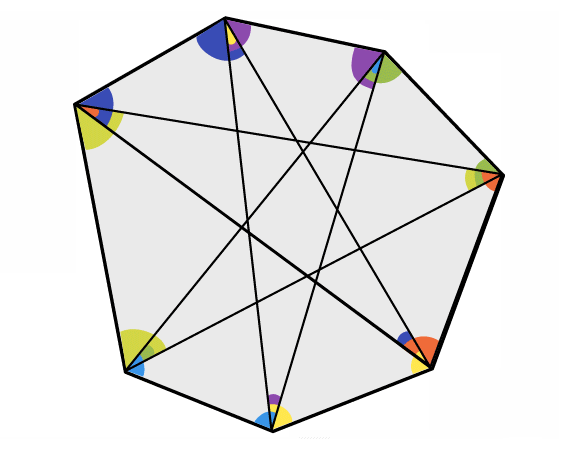
Here is a seven-pointed star:
Draw some seven-pointed stars of your own.
Measure the interior angles at the seven points and add them together.
What do you notice? Can you explain your findings?
You might find the animation below helpful:
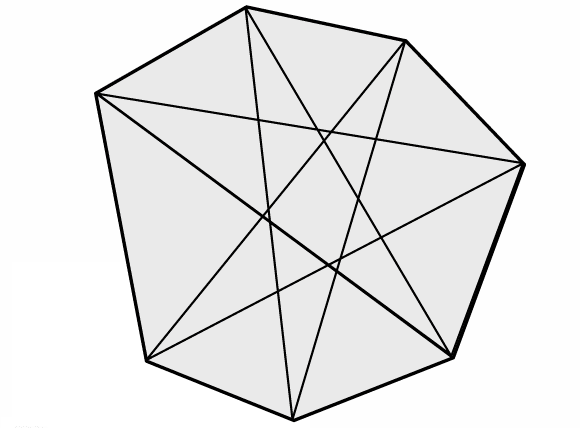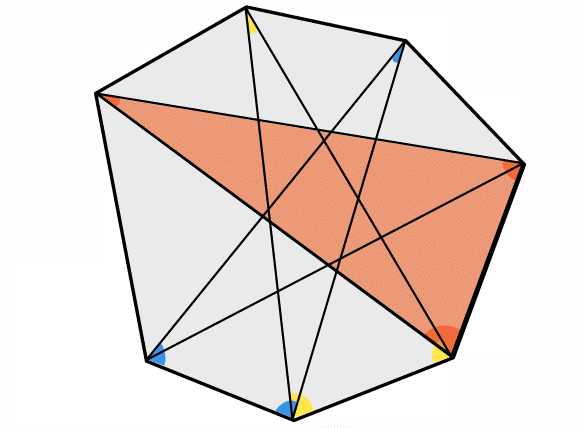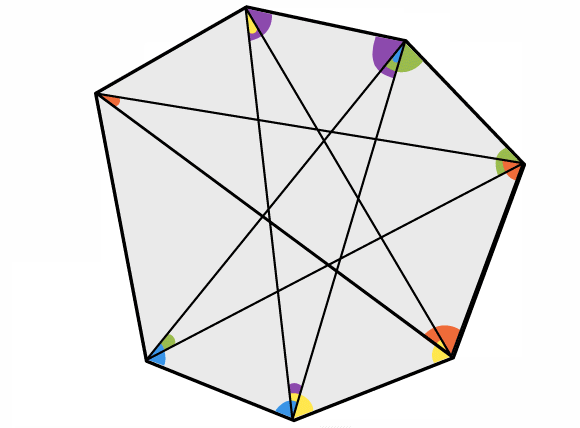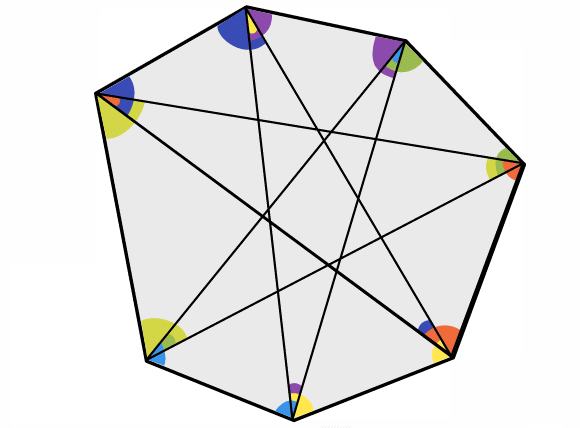
Click below to reveal a picture from the end of the animation:
Can you state and prove similar results for any other types of stars?
You may also like
Arclets Explained
This article gives an wonderful insight into students working on the Arclets problem that first appeared in the Sept 2002 edition of the NRICH website.
Bow Tie
Show how this pentagonal tile can be used to tile the plane and describe the transformations which map this pentagon to its images in the tiling.