The Third Dimension

Lots of you sent us excellent solutions for The Third Dimension. Chris and Michael from Moorfield Junior School, and Lily and Ruth from Brecknock Primary School in Camden managed to find eight arrangements altogether, including the one which we drew in the question. Lily explains how she systematically looked for them all:

To do this problem I used unifix cubes to help me. First I started with a long block, then I took one cube off and moved it to different positions making sure I didn't do the same one twice. I kept the cube in the middle and moved a second cube from the end to make a square. After that I moved this brick into further positions.

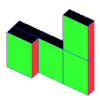
Here is Ruth's drawing which shows these arrangements very clearly:

Ciara (from Bristol) explained her strategy:

First I built a tower with multilink where all four blocks were in a row. I called this 'The Tower'. Then I kept three in a row and moved one block into other possible positions. I gave them both names and this helped me with spotting if I'd done any repeats.

When I'd found all of these, I tried versions where there were no more than two blocks in a row. The names were really useful especially with the 'Staircases' as I realised there were two different ways of building the staircase.

In total I found 8 different possibilities for arranging four cubes.


Thank you for these good solutions. Well done !