Polygon Pictures

We received lots of excellent solutions to this problem, so thank you to Peter from Durham Johnston School in Durham, Tom, Ronan, Carmi, Nardia, Bryn, Justin, Vivek, Priya, Aden, Tegan and Lucy from St Stephen's School Carramar in Australia, Aleks from Inter Community School Zurich in Switzerland, Mahdi from Mahatma Gandhi International School in India and Berkeley from Mary Hogan Elementary School in the USA for sending us your solutions.

Peter, Aleks and Berkeley sent us clear explanations of how to find the angle of rotation for each of the pictures. This is Peter's explanation.

I looked at the diagrams constructed of different polygons. The first diagram was constructed of $9$ hexagons around a point. The angle around a point is equal to $360^\circ$. Therefore, to find out the angle of rotation I divided by $9$ to get $360^\circ \div 9 = 40^\circ$. So the angle of rotation is $40^\circ$.

The second diagram was constructed of $8$ pentagons around a point. So, as before, I divided $360$ by $8$ to get $360^\circ \div 8 = 45^\circ$. So the angle of rotation is $45^\circ$.


Ronan sent us an explanation of how to find most of the angles in the first picture. 

 

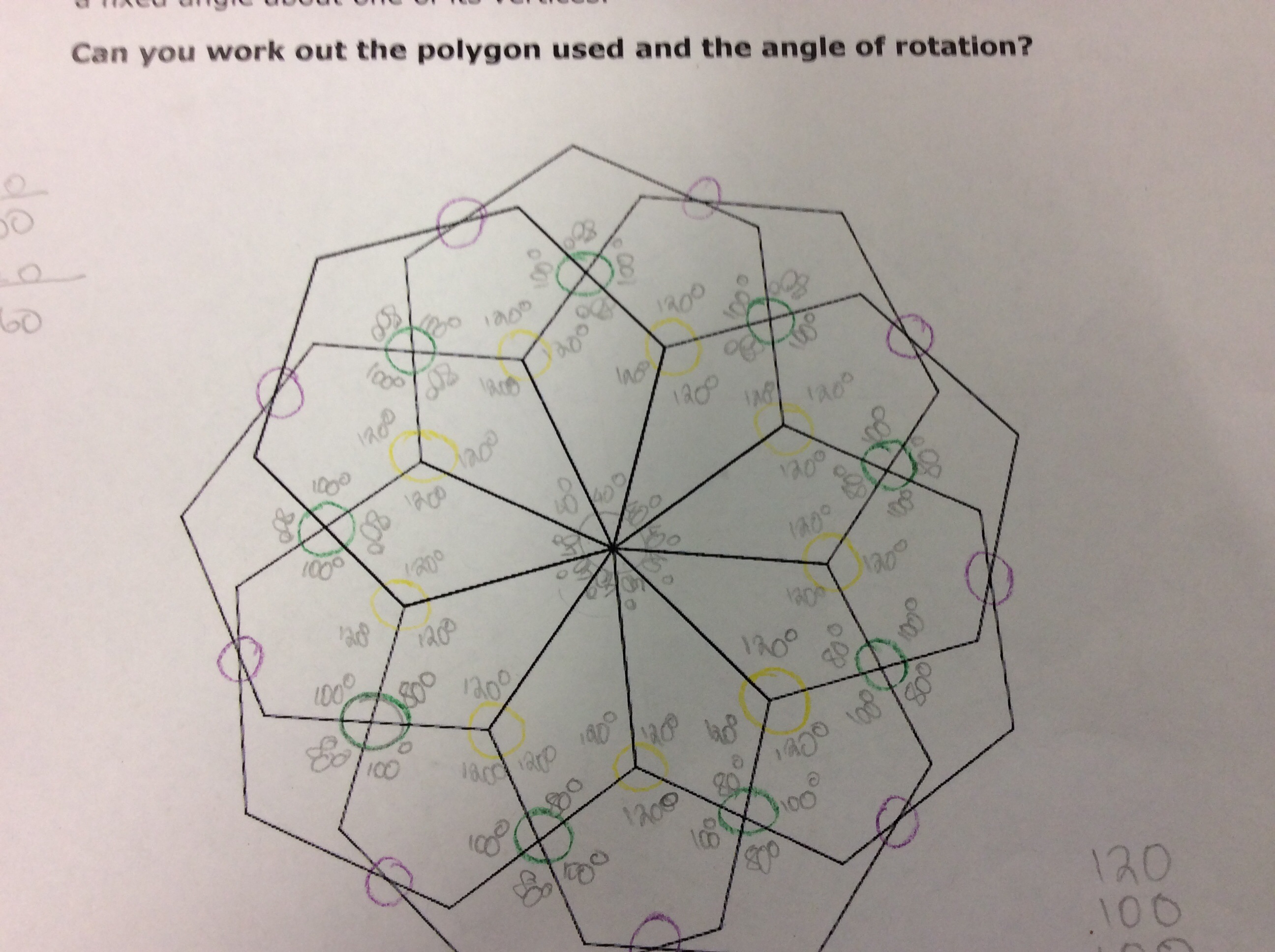
To figure out the angles on the around the middle of the shape, I divided $360$ by $9$. This is because I know the full circle is $360^\circ$ and there were $9$ angles. This brought me to find out that all the angles around the middle of the shape are $40^\circ$ each.

To find the yellow angles I noticed that two of the angles were interior angles from the regular hexagons, which are each $120^\circ$. So I subtracted these from $360^\circ$ to find the third angle. This gave me $360^\circ - 120^\circ \times 2 = 120^\circ$. So each of the yellow angles are $120^\circ$.

To figure out the green angles, I looked at the previous yellow angles and the middle angles that I had just done. As there are four angles in the kite, they all have to add up to $360^\circ$. The other angles in the kite add up to $40^\circ + 120^\circ \times 2 = 280^\circ$. This means that the last angle in the kite has to be $360^\circ - 280^\circ = 80^\circ$. The vertically opposite angle must be the same. These two $80^\circ$ angles add up to $160^\circ$ which means we need $360^\circ - 160^\circ = 200^\circ$ from the other two angles (in order to make $360^\circ$). This means the other angles are $200^\circ \div 2 = 100^\circ$ each.


Vivek offered us a method of finding the rest of the angles in the first picture. He begins by finding the purple angles from Ronan's diagram.

To find the remaining three angles in the irregular hexagon, we first notice that two of the remaining angles are interior angles of the regular hexagons, so they must be $120^\circ$. Since the interior angles in any hexagon add up to $720^\circ$, this is also true for the irregular hexagon. So the last angle is $720^\circ - 120^\circ \times 3 - 100^\circ \times 2 = 160^\circ$.

We can now find the angles for the concave hexagon (the shape on top of the kite). We already know that the angle vertically opposite the kite is $80^\circ$. From the irregular hexagon, we can also find the remaining acute angles of the concave hexagon. The vertically opposite angle must also be $160^\circ$, so since the angles around a point add up to $360^\circ$, we know that the acute angles we are looking for must be $\frac{360^\circ - 160^\circ \times 2}{2} = 20^\circ$. From what we know about the irregular hexagon, we can also find the reflex angles in the concave hexagon, which are $360^\circ - 120^\circ = 240^\circ$. We now have five of the angles for the concave hexagon, so we can just use the interior angle sum to find the top angle in the concave hexagon: $720^\circ - 80^\circ - 20^\circ \times 2 - 240^\circ \times 2 = 120^\circ$.


Mahdi sent us this detailed and clear explanation of how to find all of the angles in the pentagon diagram.