Skip over navigation
Answer: 250
The sequence of hexagon lines
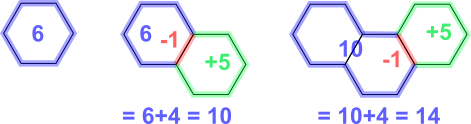
1-hexagon line has perimeter of 6
Each hexagon adds 4 to the perimeter
$\therefore$ perimeter = 6 + 4$\times$ number of hexagons added
So 1002 = 6 + 4$\times$?
$\Rightarrow$ 996 = 4$\times$?
996$\div$4 = 249
The perimeter is 1002 cm when 249 hexagons have been added to the first hexagon, so there are 250 hexagons altogether
Counting the lines in the pattern
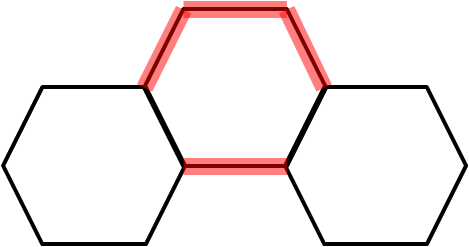 End hexagons contribute 5 cm to perimeter
End hexagons contribute 5 cm to perimeter
Non-end hexagons contribute 4 cm to perimeter
2 end hexagons contribute 10 cm to the perimeter
$\therefore$ the non-end hexagons contribute 1002$-$10 = 992 cm to the perimeter
992$\div$4 = 248
There are 248 non-end hexagons and 2 end hexagons = 250 hexagons in total
Alternatively, notice that each hexagon contributes $4$cm to the total perimeter, except the end two which contribute $2$ extra cm ($1$cm each), so if we take $2$cm off the total perimeter and divide by $4$ we will have the total number of hexagons in our shape. This gives us $n=250$.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Hexagon Line
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Answer: 250
The sequence of hexagon lines

1-hexagon line has perimeter of 6
Each hexagon adds 4 to the perimeter
$\therefore$ perimeter = 6 + 4$\times$ number of hexagons added
So 1002 = 6 + 4$\times$?
$\Rightarrow$ 996 = 4$\times$?
996$\div$4 = 249
The perimeter is 1002 cm when 249 hexagons have been added to the first hexagon, so there are 250 hexagons altogether
Counting the lines in the pattern
 End hexagons contribute 5 cm to perimeter
End hexagons contribute 5 cm to perimeterNon-end hexagons contribute 4 cm to perimeter
2 end hexagons contribute 10 cm to the perimeter
$\therefore$ the non-end hexagons contribute 1002$-$10 = 992 cm to the perimeter
992$\div$4 = 248
There are 248 non-end hexagons and 2 end hexagons = 250 hexagons in total
Alternatively, notice that each hexagon contributes $4$cm to the total perimeter, except the end two which contribute $2$ extra cm ($1$cm each), so if we take $2$cm off the total perimeter and divide by $4$ we will have the total number of hexagons in our shape. This gives us $n=250$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

