Luis' Eight

Answer: $48$ 


Using symbols

Luis' numbers: $n$, $n+1$, $n+2$, $n+3$, $n+4$, $n+5$, $n+6$ and $n+7$

The sum of the three smallest numbers: $n+(n+1)+(n+2) = 3n+3$

The sum of the three largest numbers: $(n+5)+(n+6)+(n+7) = 3n+18$

Three smallest numbers add up to $33$ so $3n+3 = 33$

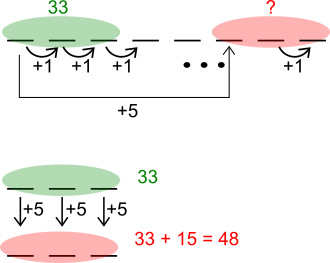
$3n+18 = (3n+ 3) + 15 = 33+15 = 48$
 

Alternatively method using symbols:

Luis' numbers: $n$, $n+1$, $n+2$, $n+3$, $n+4$, $n+5$, $n+6$ and $n+7$

The sum of the three smallest numbers: $n+(n+1)+(n+2) = 3n+3$

Three smallest numbers add up to $33$, so $3n+3 = 33$, so $n = 10$

So Luis' numbers are: $10$, $11$, $12$, $13$, $14$, $15$, $16$ and $17$

The sum of the three largest numbers: $15+16+17 = 48$


Thinking about patterns in the numbers: