Skip over navigation
Answer: 30, if the slices are all the same size
10, if the slices can be differently sized
Grandma needs to have a number of pieces of cake that is divisible by $3$, $5$ and $6$. The smallest such number will be the Lowest Common Multiple of these numbers.
$3$ and $5$ are prime numbers, whilst $6$ factorises as $2 \times 3$. The lowest common multiple will therefore have prime factorisation $2 \times 3 \times 5$.
This means the lowest common multiple will be $30$, so Grandma should cut her cake into $30$ pieces.
Michael Hatch sent us two alternative solutions:
As the wording of the question states each child must have the same AMOUNT of cake, not the same number of slices, and there is also no condition that the pieces need to be cut into the same sized slices, this creates a different solution.
Only 10 slices of cake are needed: 5 slices of $60^\circ$ and 5 slices of $12^\circ$.
3 grandchildren: 2 have 2 slices of $60^\circ$, 1 has 1 slice of $60^\circ$ and 5 slices of $12^\circ$.
5 grandchildren: each has 1 slice of $60^\circ$ and 1 slice of $12^\circ$.
6 grandchildren: 5 have 1 slice of $60^\circ$ and 1 has 5 slices of $12^\circ$.
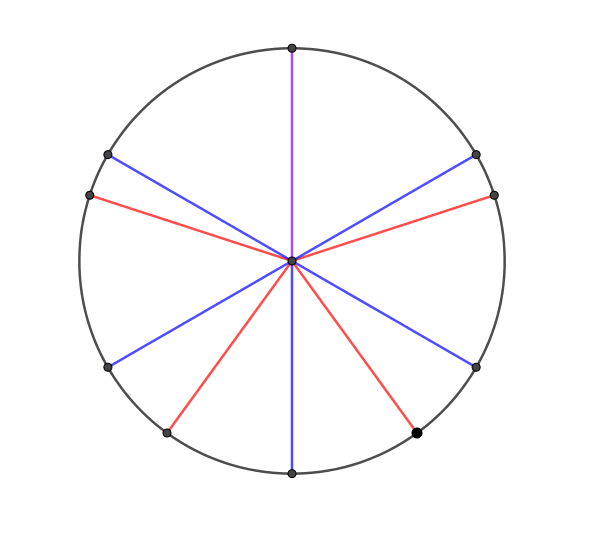
Fred also suggested a way of cutting the cake into just 10 slices:
Grandma's Cake
Age 11 to 14
ShortChallenge Level 
Answer: 30, if the slices are all the same size
10, if the slices can be differently sized
Grandma needs to have a number of pieces of cake that is divisible by $3$, $5$ and $6$. The smallest such number will be the Lowest Common Multiple of these numbers.
$3$ and $5$ are prime numbers, whilst $6$ factorises as $2 \times 3$. The lowest common multiple will therefore have prime factorisation $2 \times 3 \times 5$.
This means the lowest common multiple will be $30$, so Grandma should cut her cake into $30$ pieces.
Michael Hatch sent us two alternative solutions:
As the wording of the question states each child must have the same AMOUNT of cake, not the same number of slices, and there is also no condition that the pieces need to be cut into the same sized slices, this creates a different solution.
Only 10 slices of cake are needed: 5 slices of $60^\circ$ and 5 slices of $12^\circ$.
3 grandchildren: 2 have 2 slices of $60^\circ$, 1 has 1 slice of $60^\circ$ and 5 slices of $12^\circ$.
5 grandchildren: each has 1 slice of $60^\circ$ and 1 slice of $12^\circ$.
6 grandchildren: 5 have 1 slice of $60^\circ$ and 1 has 5 slices of $12^\circ$.
Fred also suggested a way of cutting the cake into just 10 slices:
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...