Skip over navigation
There are a number of different ways of solving this problem.
Directions
The number of vertical rhombi can be seen by looking at the possible positions of the top triangle. The following six rhombi are then apparrent.
The problem has rotational symmetry, so the other two directions will also give six rhombi each.
This means that the total number of rhombi is $3 \times 6 = 18$.
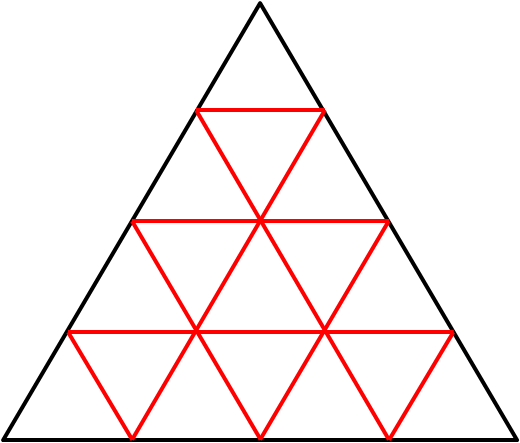Interior Edges
Each rhombus that is formed has exactly one of the interior edges (marked in red) contained within it. Moreover, each interior edge corresponds to one rhombus, consisting of the triangles on either side. There are $18$ interior edges, so $18$ rhombi that can be formed.
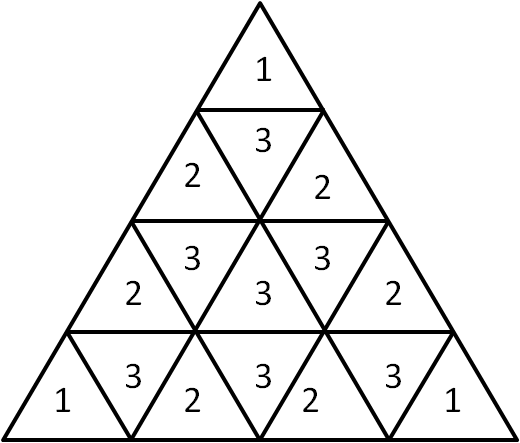Double-counting
For each of the small triangles, the number of rhombi that contain it can be counted, as shown in the diagram on the right. However, this counts each rhombus twice (once for each triangle it contains). Therefore the total obtained ($36$) must be halved, giving a total of $18$ rhombi.
Isometric Rhombuses
Age 11 to 14
ShortChallenge Level 
There are a number of different ways of solving this problem.
DirectionsThe number of vertical rhombi can be seen by looking at the possible positions of the top triangle. The following six rhombi are then apparrent.
The problem has rotational symmetry, so the other two directions will also give six rhombi each.
This means that the total number of rhombi is $3 \times 6 = 18$.
Interior EdgesEach rhombus that is formed has exactly one of the interior edges (marked in red) contained within it. Moreover, each interior edge corresponds to one rhombus, consisting of the triangles on either side. There are $18$ interior edges, so $18$ rhombi that can be formed.
Double-countingFor each of the small triangles, the number of rhombi that contain it can be counted, as shown in the diagram on the right. However, this counts each rhombus twice (once for each triangle it contains). Therefore the total obtained ($36$) must be halved, giving a total of $18$ rhombi.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Tea Cups
Place the 16 different combinations of cup/saucer in this 4 by 4 arrangement so that no row or column contains more than one cup or saucer of the same colour.
Counting on Letters
The letters of the word ABACUS have been arranged in the shape of a triangle. How many different ways can you find to read the word ABACUS from this triangular pattern?