Skip over navigation
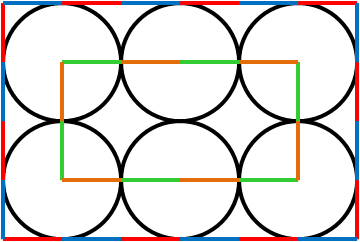The small rectangle consists of $12$ of the radii of the circles, each connecting a point of contact to the centre of the relevant circle. These are shown in green and orange in the diagram on the right.
Since this has a total length of $60\text{cm}$, each radius is of length $60\text{cm} \div 12 = 5\text{cm}$.
The large rectangle can also be broken down into segments of this length. These are shown in blue and red on the diagram. There are $20$ of these, so the perimeter of the large rectangle is $5\text{cm} \times 20 = 100\text{cm} = 1\text{m}$.
Six Circles
Age 11 to 14
ShortChallenge Level 
The small rectangle consists of $12$ of the radii of the circles, each connecting a point of contact to the centre of the relevant circle. These are shown in green and orange in the diagram on the right.Since this has a total length of $60\text{cm}$, each radius is of length $60\text{cm} \div 12 = 5\text{cm}$.
The large rectangle can also be broken down into segments of this length. These are shown in blue and red on the diagram. There are $20$ of these, so the perimeter of the large rectangle is $5\text{cm} \times 20 = 100\text{cm} = 1\text{m}$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Hallway Borders
What are the possible dimensions of a rectangular hallway if the number of tiles around the perimeter is exactly half the total number of tiles?
