How Many Rectangles?

Answer: 42


The sequence of patterns
 

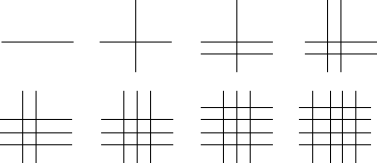
Number of lines	New rectangles
1	0
2	0
3	0
4	1
5	1
6	2
7	2
8	3

You add more rectangles horizontally, then vertically, so the pattern continues.
9th line adds 3 rectangles (already seen that 9 lines make12 rectangles)
10th, 11th lines   +4 each      total 12 + 8 = 20
12th, 13th lines   +5 each      total 20 + 10 = 30
14th, 15th lines   +6 each      total 30 + 12 = 42


An expression for the number of rectangles
Suppose there are $a$ horizontal and $b$ vertical lines. The grid of rectangles formed is then $a-1$ rectangles high, and $b-1$ rectangles wide. This means there are $(a-1)(b-1)$ rectangles.

If there are a total of $15$ lines, the aim is to make $(a-1)(b-1)$ as large as possible with $a+b=15$.

This can be done by considering the different combinations that add to make $15$:

$a$	$b$	$(a-1)(b-1)$
$1$	$14$	$0 \times 13 = 0$
$2$	$13$	$1 \times 12 = 12$
$3$	$12$	$2 \times 11 = 22$
$4$	$11$	$3 \times 10 = 30$
$5$	$10$	$4 \times 9 = 36$
$6$	$9$	$5 \times 8 = 40$
$7$	$8$	$6 \times 7 = 42$

Therefore, the largest number is $42$ rectangles, formed by having seven lines in one direction and eight in the other.



Alternatively, you can use completing the square to maximise the quantity:

Since $a+b=15$, $(a-1)(b-1) = (a-1)(14-a) = -a^2+15a-14$. Then, by completing the square, this is $-\left(a-\frac{15}{2}\right)^2 + \frac{169}{4}$.

This is maximised when the square is minimised, which occurs when $a=7$ or $a=8$ (since $a$ must be an integer). This gives $6 \times 7 = 42$ rectangles.