Skip over navigation
Answer: 6
Here are two possible ways of thinking about this problem, although there are many other possibilities.
Choosing the colour of the top triangle
If the top triangle is painted black, there are three choices for the other black triangle, then the other two are painted white.
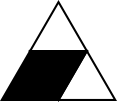
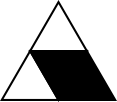If on the other hand the top triangle is painted white, there are three choices for the other white triangle, with the other two painted black. This gives a total of
If not and the left hand triangle is painted black, the other black triangle could be the centre or right-hand
triangles, so $2$ choices
If the top and left are both white, the other two triangles are both black.
This means there are $3+2+1=6$ possibilities.
This problem is looking at the number of ways to choose two of the four triangles to paint black. This can be written as $^4C_2$ or $4 \choose 2$, which are called binomial coefficiants. If you want to find out more about these, then you can look at this article.
Half and Half
Age 11 to 14
ShortChallenge Level 
Answer: 6
Here are two possible ways of thinking about this problem, although there are many other possibilities.
Choosing the colour of the top triangle
If the top triangle is painted black, there are three choices for the other black triangle, then the other two are painted white.If on the other hand the top triangle is painted white, there are three choices for the other white triangle, with the other two painted black. This gives a total of $6$ possibilities.
Choosing which triangles are black
If the top triangle is painted black, there are three choices for the other black triangle.
Choosing which triangles are black
If the top triangle is painted black, there are three choices for the other black triangle.If not and the left hand triangle is painted black, the other black triangle could be the centre or right-hand
triangles, so $2$ choicesIf the top and left are both white, the other two triangles are both black.This means there are $3+2+1=6$ possibilities.
This problem is looking at the number of ways to choose two of the four triangles to paint black. This can be written as $^4C_2$ or $4 \choose 2$, which are called binomial coefficiants. If you want to find out more about these, then you can look at this article.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Tea Cups
Place the 16 different combinations of cup/saucer in this 4 by 4 arrangement so that no row or column contains more than one cup or saucer of the same colour.
Counting on Letters
The letters of the word ABACUS have been arranged in the shape of a triangle. How many different ways can you find to read the word ABACUS from this triangular pattern?