Skip over navigation
Answer: 7
Using totals
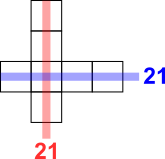
21 + 21 = 42
2 + 3 + 4 + 5 + 6 + 7 + 8 = 35
7 missing so the 7 is couted twice
x = 7
Using totals and symbols
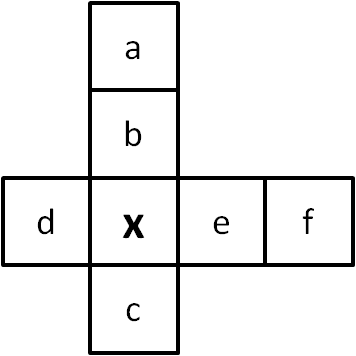The cells in the diagram can each be assigned a letter. Since the row and column both sum to $21$, this gives the equations:
Then, the letters $a$, $b$, $c$, $d$, $e$, $f$ and $x$ are, in some order, $2$, $3$, $4$, $5$, $6$, $7$ and $8$. This means that their sums must be the same, so;$$a+b+c+d+e+f+x = 2+3+4+5+6+7+8 = 35.$$ Then, if the equations at the top are added together, these give:$$a+b+c+d+e+f+2x=42.$$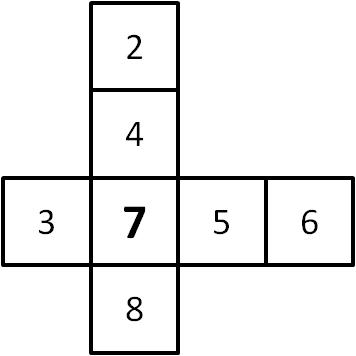
But then, subtracting the previous equation from this one gives $x = 7$, as all the other terms cancel out.
Crossover
Age 11 to 14
ShortChallenge Level 
Answer: 7
Using totals
21 + 21 = 42
2 + 3 + 4 + 5 + 6 + 7 + 8 = 35
7 missing so the 7 is couted twice
x = 7
Using totals and symbols
The cells in the diagram can each be assigned a letter. Since the row and column both sum to $21$, this gives the equations:$a+b+x+c = 21$
$d+x+e+f = 21$
$d+x+e+f = 21$
Then, the letters $a$, $b$, $c$, $d$, $e$, $f$ and $x$ are, in some order, $2$, $3$, $4$, $5$, $6$, $7$ and $8$. This means that their sums must be the same, so;$$a+b+c+d+e+f+x = 2+3+4+5+6+7+8 = 35.$$ Then, if the equations at the top are added together, these give:$$a+b+c+d+e+f+2x=42.$$
But then, subtracting the previous equation from this one gives $x = 7$, as all the other terms cancel out.This value of $x$ can be achieved as shown in the diagram on the right.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...