Skip over navigation
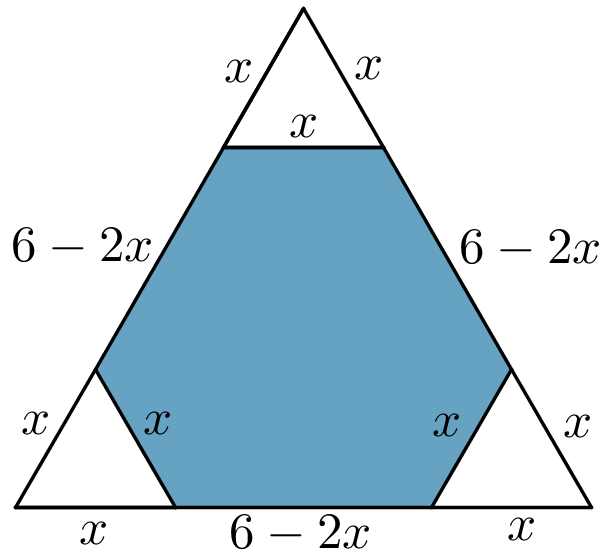Suppose the small equilateral triangles have sides of length $x\text{cm}$. Then, each of these has perimeter $3x$, and there are three of these, so the total perimeter is $3 \times 3x = 9x$.
The hexagon has three sides where the triangles have been cut from, each of length $x$. The other sides are the sides of the larger triangle, less two sides of the smaller triangles. They, therefore, have length $6-2x$. There are three of each of these, so the perimeter of the hexagon is $3x + 3(6-2x)$.
Since the hexagon has a perimeter equal to the sum of the three small triangles, we get:
Then, expanding the bracket gives:
Collecting like terms:
Adding $3x$ to each side:
Dividing by $6$:
Therefore, the small equilateral triangles have sides of length $1.5\text{cm}$.
Corner Cut
Age 11 to 14
ShortChallenge Level 
Suppose the small equilateral triangles have sides of length $x\text{cm}$. Then, each of these has perimeter $3x$, and there are three of these, so the total perimeter is $3 \times 3x = 9x$.The hexagon has three sides where the triangles have been cut from, each of length $x$. The other sides are the sides of the larger triangle, less two sides of the smaller triangles. They, therefore, have length $6-2x$. There are three of each of these, so the perimeter of the hexagon is $3x + 3(6-2x)$.
Since the hexagon has a perimeter equal to the sum of the three small triangles, we get:
$9x = 3x + 3(6-2x)$
Then, expanding the bracket gives:
$9x = 3x + 18 - 6x$
Collecting like terms:
$9x = 18 - 3x$
Adding $3x$ to each side:
$12x = 18$
Dividing by $6$:
$x = 1.5$
Therefore, the small equilateral triangles have sides of length $1.5\text{cm}$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Hallway Borders
What are the possible dimensions of a rectangular hallway if the number of tiles around the perimeter is exactly half the total number of tiles?
