Skip over navigation
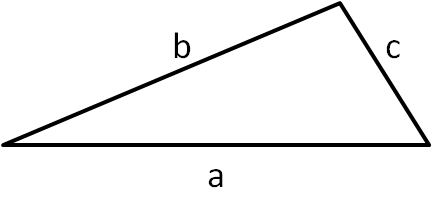 For this problem, we need to use the triangle inequality. Although this might sound scary, all it is saying is that the shortest route between two points is the straight line that joins them. For example, in the diagram on the right, the shortest distance between
the bottom-left and bottom-right vertices is via the bottom edge. This is shorter than walking around the other two edges.
For this problem, we need to use the triangle inequality. Although this might sound scary, all it is saying is that the shortest route between two points is the straight line that joins them. For example, in the diagram on the right, the shortest distance between
the bottom-left and bottom-right vertices is via the bottom edge. This is shorter than walking around the other two edges.
Algebraically, this can be written as $a < b+c$. The same is true for the other sides, so $b < a+c$ and $c < a+b$ also.
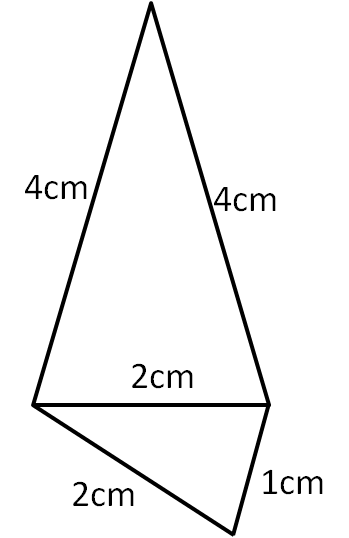 In the problem, the two isosceles triangles must each consist of the diagonal, together with two of the sides of the quadrilateral.
In the problem, the two isosceles triangles must each consist of the diagonal, together with two of the sides of the quadrilateral.
One of these must have both the diagonal of length $2\text{cm}$ and the side of length $1\text{cm}$. Since this triangle is isosceles, two of the sides have the same length, so the other side is either $1\text{cm}$ or $2\text{cm}$.
However, the triangle inequality says that the $2\text{cm}$ side must be shorter than the sum of the other two sides. This means the third side must be of length $2\text{cm}$.
We can do the same thing looking at the other isosceles triangle. This has a side of length $2\text{cm}$ and a side of length $4\text{cm}$. The triangle inequality says that the other two sides must together be longer than the $4\text{cm}$ side, so the unknown side must be longer than $2\text{cm}$. To make the triangle isosceles, the final side must also have length $4\text{cm}$.
This gives the quadrilateral in the diagram on the right. The perimeter of this is $4+4+1+2=11\text{cm}$.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Two Isosceles
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
 For this problem, we need to use the triangle inequality. Although this might sound scary, all it is saying is that the shortest route between two points is the straight line that joins them. For example, in the diagram on the right, the shortest distance between
the bottom-left and bottom-right vertices is via the bottom edge. This is shorter than walking around the other two edges.
For this problem, we need to use the triangle inequality. Although this might sound scary, all it is saying is that the shortest route between two points is the straight line that joins them. For example, in the diagram on the right, the shortest distance between
the bottom-left and bottom-right vertices is via the bottom edge. This is shorter than walking around the other two edges.Algebraically, this can be written as $a < b+c$. The same is true for the other sides, so $b < a+c$ and $c < a+b$ also.
 In the problem, the two isosceles triangles must each consist of the diagonal, together with two of the sides of the quadrilateral.
In the problem, the two isosceles triangles must each consist of the diagonal, together with two of the sides of the quadrilateral.One of these must have both the diagonal of length $2\text{cm}$ and the side of length $1\text{cm}$. Since this triangle is isosceles, two of the sides have the same length, so the other side is either $1\text{cm}$ or $2\text{cm}$.
However, the triangle inequality says that the $2\text{cm}$ side must be shorter than the sum of the other two sides. This means the third side must be of length $2\text{cm}$.
We can do the same thing looking at the other isosceles triangle. This has a side of length $2\text{cm}$ and a side of length $4\text{cm}$. The triangle inequality says that the other two sides must together be longer than the $4\text{cm}$ side, so the unknown side must be longer than $2\text{cm}$. To make the triangle isosceles, the final side must also have length $4\text{cm}$.
This gives the quadrilateral in the diagram on the right. The perimeter of this is $4+4+1+2=11\text{cm}$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

