Who's Who?

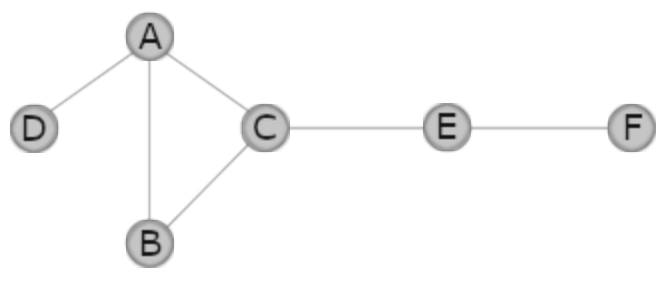
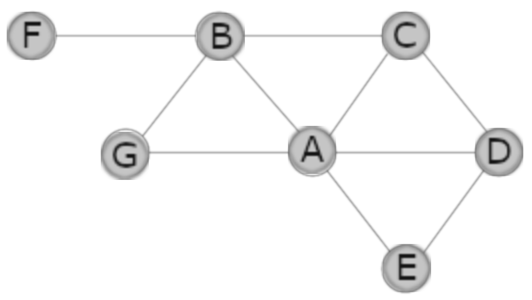
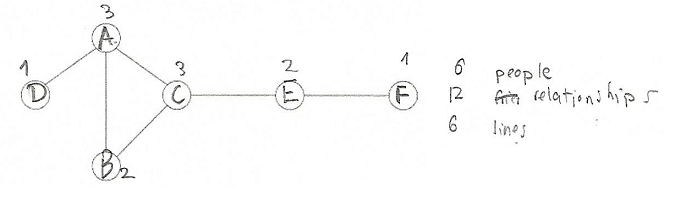
Ansh from Cherrybrook Technology High School in Australia, Neel from Zurich International School in Switzerland and Ethan from England completed the first graph. Here is Ansh's screenshot:

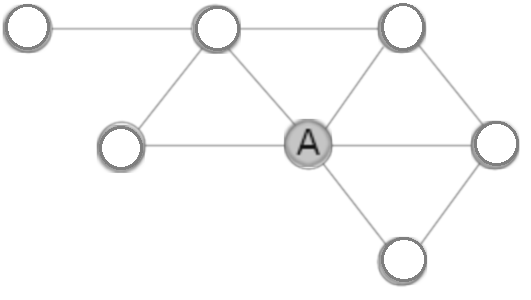
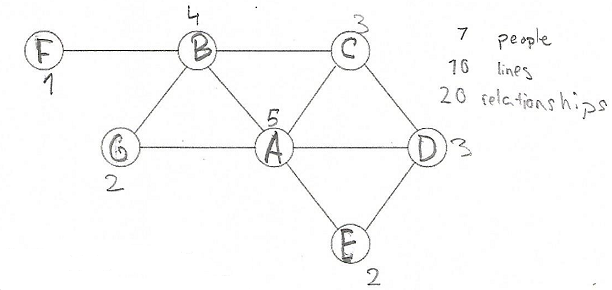
Jamie and Wally from Twyford School in England, Ansh, Neel, Ethan completed the second graph. This is Jamie and Wally's work, including their reasoning:

A can only be in the middle because A has the most amount of friends and that is only in the middle with 5 friend.

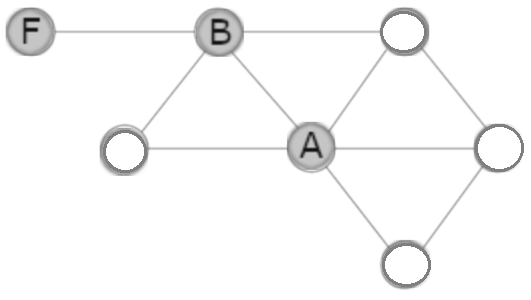
B can only be there because it has to be next to F and has one friend so F has to be next to B.

C can only be there because C has 3 friends and is friends with B (and not friends with E).

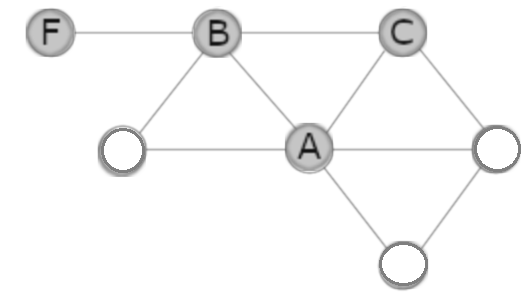
E  has to go there because E has 2 friends, G and D are not friends so G has to go there.

Willa from Twyford School answered the questions about the problems:

Did each problem have a unique solution? 
Yes each problem has a unique solution. I can see this because the majority of letters in each problem have to be in a fixed position. They cannot move. For example A has to be in the middle because that is the one connected with the most friends. 

Were there any clues you didn't need to use?
I do not think there were any clues that I did not need to use. This is because they are all useful when it comes to checking over your work. Although I think each problem has clues which are more useful than the others. For instance in the first problem the first and third clue was more useful than the second. 

If you label each node with the number of friends the person has, and add together all the numbers, what can you say about the answer? Can you explain why?
When you add together the number of friends each person has in the second question you find that there are more friends than people. This is because lots of people have more than one friend and they are all are the same.
 

Neel did some more work on adding up the numbers of friends each person has:

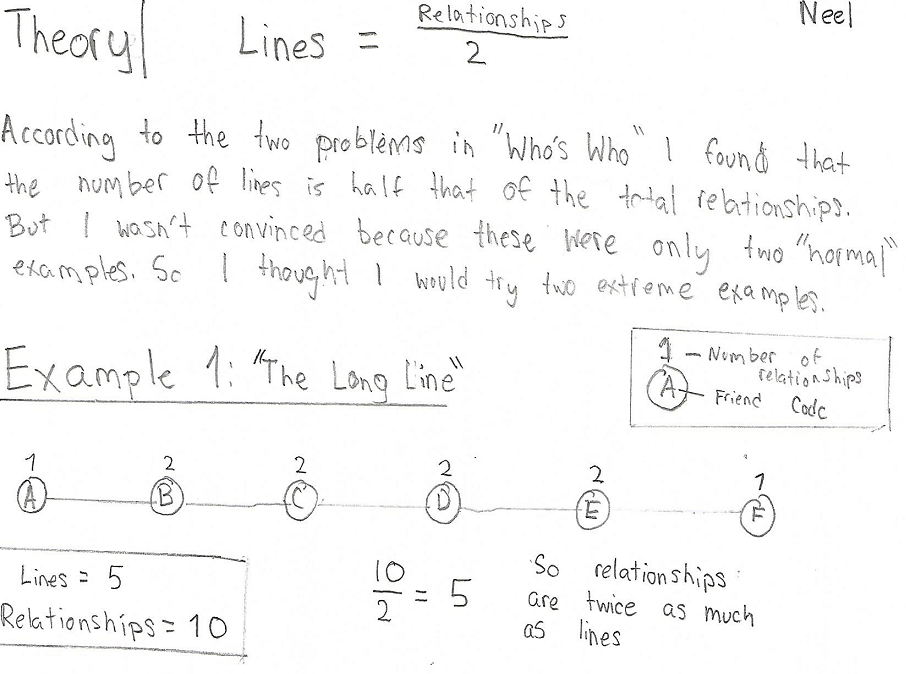
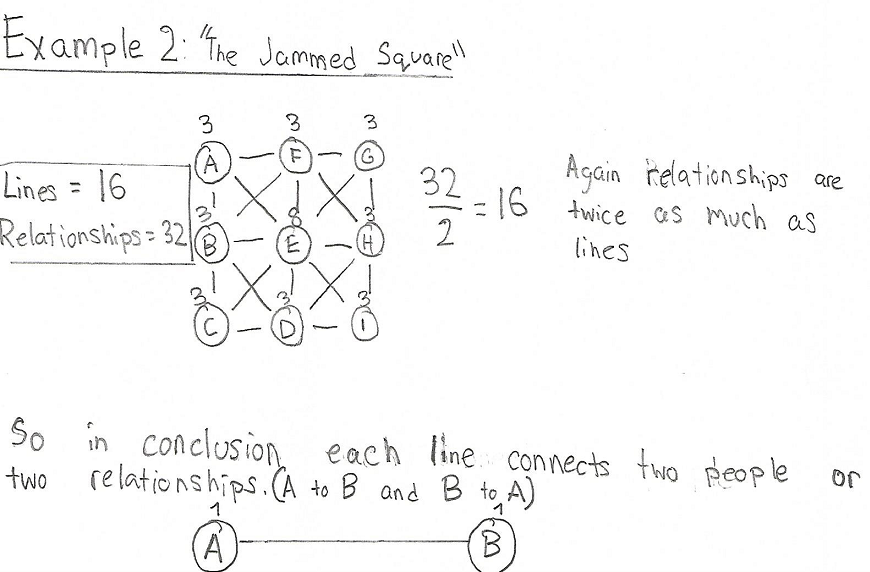
Well done to everyone!