Skip over navigation
Vignesh and Amrit from Hymers College in the UK sent in proofs which use the same reasoning.
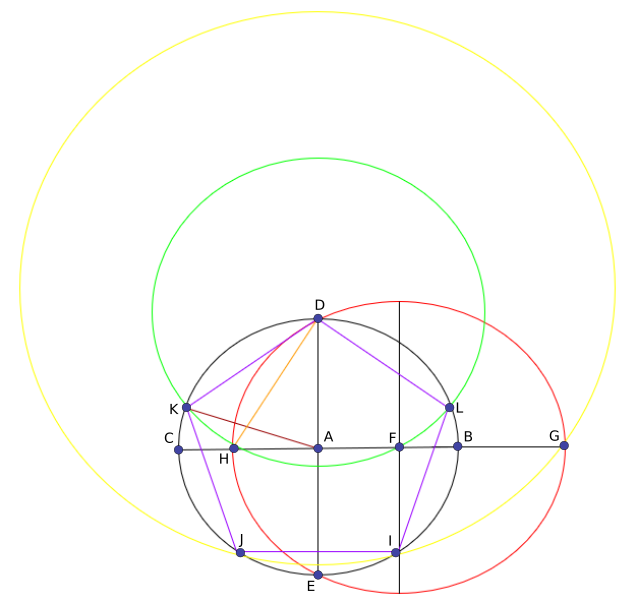
This is Vignesh's diagram, with the names of the points added.
This is the beginning of Amrit's proof:
Let the radius of the circle $C_1$ (black in Vignesh's diagram) with centre at point $\text A$ passing through point $\text B$ be $1.$
Vignesh made a different choice:
$R_0 = \text{AB}$ (radius of black circle)
Let $R_0 = x$
Vignesh calls the distance $\text{AB}$ $x$, because it is unknown, but Amrit says it is $1.$ Changing the length $\text{AB}$ will rescale the diagram, but it won't affect whether the pentagon is regular, so it doesn't matter how long $\text{AB}$ is. This is why it is safe for Amrit to choose that $\text{AB}=1.$ Vignesh also chose this length at the beginning of the constuction, because it starts with two points $\text{A}$ and $\text{B}$ - and Vignesh had to choose how far apart to put them.
Using $1$ instead of $x$ makes the proof simpler, so here is the rest of Amrit's proof:
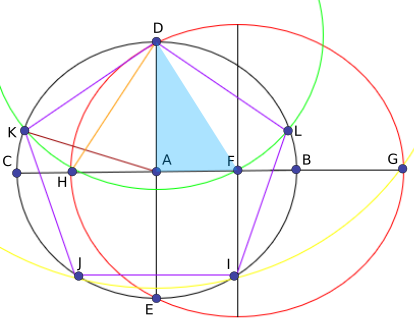 The right angled triangle $\text{FAD}$ was apparent to me when I completed the construction. By Pythagoras' theorem,
The right angled triangle $\text{FAD}$ was apparent to me when I completed the construction. By Pythagoras' theorem,
$\text{DF}=\dfrac{\sqrt5}{2}$
Then, I saw the right angled triangle $\text{ADG}$. By Pythagoras' theorem,
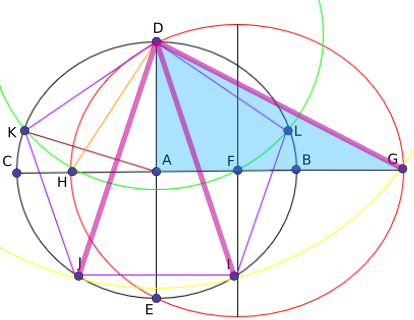
And, since $\text{DF}$ and $\text{GF}$ are both radii of the circle with centre $\text F$ passing through the point $\text D$ (red), $\text{GF}=\text{DF}=\frac{\sqrt5}{2},$ so $\text{AG}=\frac{\sqrt5}{2}+\frac{1}{2}=\frac{\sqrt5+1}{2}.$ $\text{DA}$ is again equal to $1.$ Substituting these values into the above equation, we obtain
$\text{DG}=\dfrac{\sqrt{10+2\sqrt5}}{2}$
$\text{DI = DJ = DG},$ since these line segments are all radii of the circle with centre $\text D$ passing through $\text G$ (yellow).
The next right angled triangle I observed was triangle $\text{AHD.}$ By Pythagoras' theorem,
$\text{DH}^2=\text{AH}^2+\text{DA}^2$
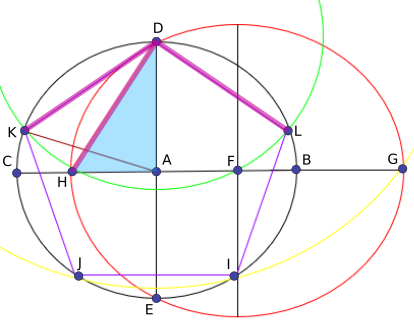 But $\text{AH}=\text{HF}-\text{FA}$
But $\text{AH}=\text{HF}-\text{FA}$
And $\text{HF}=\text{DF}=\frac{\sqrt5}{2}$, since they are both radii of the circle with centre $\text F$ that passes through $\text D$ (red). So $\text{AH}=\frac{\sqrt5}{2}-\frac{1}{2}=\frac{\sqrt5-1\ }{2}.$ $\text{DA}$ is again equal to $1.$ Substituting these values into the above equation, we obtain
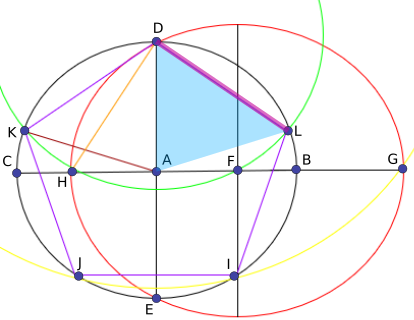 We can now find the size of $\angle \text{ DAL}$ using the cosine rule:
We can now find the size of $\angle \text{ DAL}$ using the cosine rule:
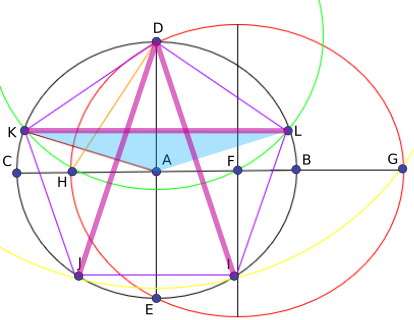 I then considered triangle $\text {ALK.}$
I then considered triangle $\text {ALK.}$
$\angle\text{ LAK}=\angle\text{ DAL}+\angle\text{ DAK}=144^\circ$
From the cosine rule, we can find the length of $\text{LK}:$
$\text{LK}=\sqrt{\text{LA}^2+\text{KA}^2-2\left(\text{LA}\right)\left(\text{KA}\right)\cos{\left(\angle \text{ LAK}\right)}}$
$\text{LA = KA}=1,$ since they are the radii of the circle $C_1$ (black), and we know that $\cos{\angle\text {LAK}}=\cos{144^\circ}=\frac{-1-\sqrt5}4.$ Substituting these values into the above equation, we obtain
$\text{LK}=\dfrac{\sqrt{10+2\sqrt5}}{2}$
So $\text{LK = DI = DJ.}$ We see then that triangle $\text{ALK}$ is congruent to triangles $\text{DAI}$ and $\text{DAJ}$ by the SSS theorem, since one side of one triangle is equal to another side of the other two triangles ($\text{LK = DI = DJ}$), and the other two sides of one triangle are equal to the other two sides of the other two triangles, because they are all radii of the circle $C_1$ (black).
In particular then, $\angle\text{ DAJ}=\angle\text{ DAI}=144^\circ.$ Also,
$\angle\text{ JAI}=360^\circ-\left(\angle\text{ DAJ}+\angle\text{ DAI}\right)$
So $\angle\text{ JAI}=72^\circ.$
Now, $\angle\text{ LAI}=\angle\text{ DAI}-\angle\text{ DAL}=72^\circ.$ Therefore, $\angle \text { KAJ}=360^\circ-\left(\angle \text{ DAK}+\angle \text{ DAL}+\angle \text{ LAI}+\angle \text{ JAI}\right)=72^\circ.$
Therefore, by the SAS congruence axiom, the triangles $\text{AIJ, AJK, AKD, ADL, ALI}$ are all congruent to each other and, in particular, $\text{IJ = JK = KD = DL = LI}$ and all the angles in one of the above triangles are equal to the angles in the corresponding four triangles, therefore $\angle\text{ I}=\angle\text{ J}=\angle\text{ K}=\angle\text{ D}=\angle\text{ L},$ where these angles are the interior angles of the shape $\text{IJKDL,}$ making this shape a regular pentagon.
It is also possible to prove that the construction gives a pentagon using coordinate geometry:
Using Cartesian coordinates with $A$ as the origin and $B$ at $(1,0)$.
Then, $D$ is at $(0,1)$, since it is the same distance away from $A$ as $B$ is but on a perpendicular line. $F$ is the midpoint of $AB$, so is at $(\frac 12,0)$.
Pythagoras' Theorem tells us that the distance $DF = \sqrt{1^2 + (\frac 12)^2} = \frac{\sqrt{5}}{2}$. Therefore $G$ is at $(\frac{1+\sqrt 5}2,0)$ and $H$ is at $(\frac{1-\sqrt 5}2,0)$.
Then, $DG = \sqrt{1^2 + \left( \frac{1+\sqrt 5}2 \right)^2} = \sqrt{1+\frac{6+2\sqrt 5}{4}} = \frac{\sqrt{10+2\sqrt{5}}}{2}$.
Then, looking at the equations of the two circles (black and yellow), we have:
\begin{eqnarray}
x^2 + y^2 &=& 1\\
x^2 + (y-1)^2 &=& \frac{5+\sqrt 5}2 \\
\end{eqnarray}
Subtracting one from the other yields:$$\begin{eqnarray}
y^2-(y-1)^2&=&1-\frac{5+\sqrt 5}{2}\\
\Rightarrow y^2-\left(y^2-2y+1\right) &=&1-\frac{5+\sqrt 5}{2}\\
\Rightarrow 2y-1 &=& 1-\frac{5+\sqrt 5}{2}\end{eqnarray}$$This has solution:$$y = -\frac{1+\sqrt 5}{2} = \cos 144^\circ$$
So $x =\pm \sin 144^\circ$, since $\left( \pm\sin 144^\circ \right) ^2 + \cos ^2 144^\circ = 1$
To use right-angled triangles, use the sine and cosine graphs to see how $\sin 144^\circ$ and $\cos 144^\circ$ compare to angles less than $90^\circ$:
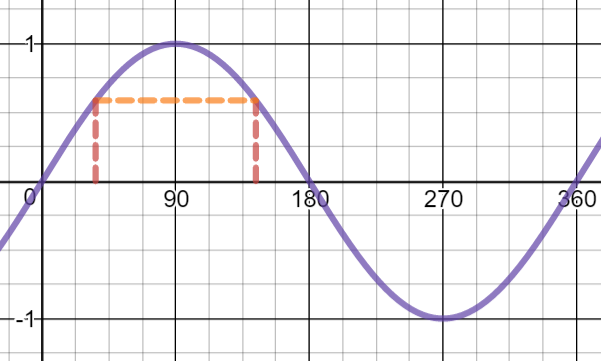
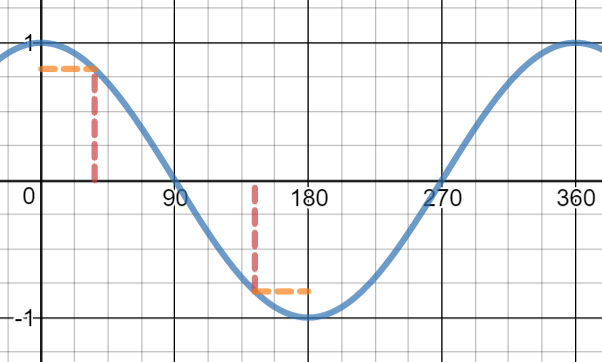
$\sin 144^\circ = \sin (90^\circ-(144^\circ-90^\circ)) = \sin 36^\circ,\cos 144^\circ = -\cos(180^\circ-144^\circ)=-\cos36^\circ$
So the points $I$ and $J$ can be plotted as shown:
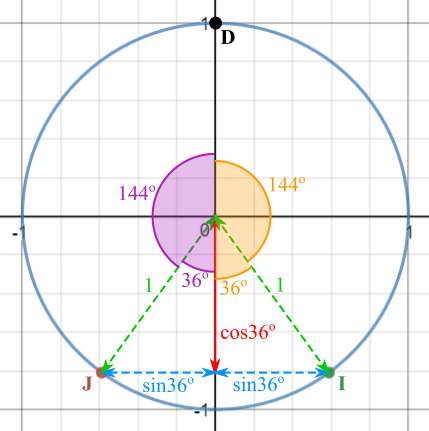
Meanwhile, $DH = \sqrt{1^2 + \left( \frac{1-\sqrt 5}2 \right)^2} = \sqrt{1+\frac{6-2\sqrt 5}{4}} = \frac{\sqrt{10-2\sqrt{5}}}{2}$.
Then, looking at the equations of the two circles, we have:
\begin{eqnarray}
x^2 + y^2 &=& 1\\
x^2 + (y-1)^2 &=& \frac{5-\sqrt 5}2 \\
\end{eqnarray}
Subtracting one from the other yields:$$2y-1 = 1-\frac{5-\sqrt 5}{2}$$This has solution:$$y = \frac{\sqrt 5-1}{2} = \cos 72^\circ$$
So $x =\pm \sin 72^\circ$, since $\left( \pm\sin 72^\circ \right) ^2 + \cos ^2 72^\circ = 1$
So the points $K$ and $L$ can be plotted as shown:
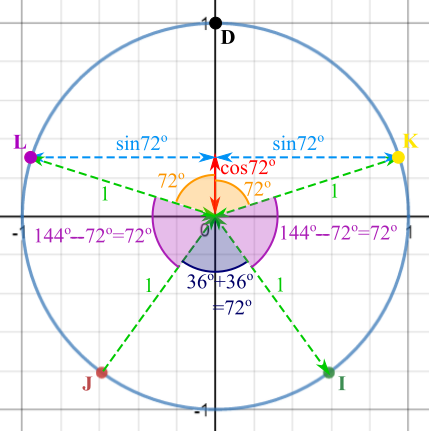
The shape $DLJIK$ is made up of five congruent isosceles triangles, so it is a regular pentagon.
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Pentagon Construction
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Vignesh and Amrit from Hymers College in the UK sent in proofs which use the same reasoning.
This is Vignesh's diagram, with the names of the points added.

This is the beginning of Amrit's proof:
Let the radius of the circle $C_1$ (black in Vignesh's diagram) with centre at point $\text A$ passing through point $\text B$ be $1.$
Vignesh made a different choice:
$R_0 = \text{AB}$ (radius of black circle)
Let $R_0 = x$
Vignesh calls the distance $\text{AB}$ $x$, because it is unknown, but Amrit says it is $1.$ Changing the length $\text{AB}$ will rescale the diagram, but it won't affect whether the pentagon is regular, so it doesn't matter how long $\text{AB}$ is. This is why it is safe for Amrit to choose that $\text{AB}=1.$ Vignesh also chose this length at the beginning of the constuction, because it starts with two points $\text{A}$ and $\text{B}$ - and Vignesh had to choose how far apart to put them.
Using $1$ instead of $x$ makes the proof simpler, so here is the rest of Amrit's proof:
 The right angled triangle $\text{FAD}$ was apparent to me when I completed the construction. By Pythagoras' theorem,
The right angled triangle $\text{FAD}$ was apparent to me when I completed the construction. By Pythagoras' theorem,$\text{DF}^2=\text{FA}^2+\text{DA}^2$
Since point F is the midpoint of the radius $\text{AB},$ $\text{FA}=\frac{1}{2}.$ Since $\text{DA}$ is a radius, $\text{DA}=1.$ Substituting these values into the above equation gives$\text{DF}=\dfrac{\sqrt5}{2}$
Then, I saw the right angled triangle $\text{ADG}$. By Pythagoras' theorem,

$\text{DG}^2=\text{DA}^2+\text{AG}^2$
But $\text{AG}=\text{GF}+\text{FA}$And, since $\text{DF}$ and $\text{GF}$ are both radii of the circle with centre $\text F$ passing through the point $\text D$ (red), $\text{GF}=\text{DF}=\frac{\sqrt5}{2},$ so $\text{AG}=\frac{\sqrt5}{2}+\frac{1}{2}=\frac{\sqrt5+1}{2}.$ $\text{DA}$ is again equal to $1.$ Substituting these values into the above equation, we obtain
$\text{DG}=\dfrac{\sqrt{10+2\sqrt5}}{2}$
The next right angled triangle I observed was triangle $\text{AHD.}$ By Pythagoras' theorem,
$\text{DH}^2=\text{AH}^2+\text{DA}^2$

And $\text{HF}=\text{DF}=\frac{\sqrt5}{2}$, since they are both radii of the circle with centre $\text F$ that passes through $\text D$ (red). So $\text{AH}=\frac{\sqrt5}{2}-\frac{1}{2}=\frac{\sqrt5-1\ }{2}.$ $\text{DA}$ is again equal to $1.$ Substituting these values into the above equation, we obtain
$\text{DH}=\dfrac{\sqrt{10-2\sqrt5}}{2}$
$\text{DL = DK = DH,}$ since these line segments are all radii of the circle with centre $\text D$ passing through $\text H$ (green). We can now find the size of $\angle \text{ DAL}$ using the cosine rule:
We can now find the size of $\angle \text{ DAL}$ using the cosine rule:$\angle \text{ DAL}=\arccos{\left(\dfrac{LA^2+DA^2-DL^2}{2\left(LA\right)\left(DA\right)}\right)}$
$\text{LA = DA}=1,$ since these line segments are both radii of the circle $C_1$ (black), and it was deduced above that $\text{DL = DH}=\dfrac{\sqrt{10-2\sqrt5}}{2}.$ Substituting these values into the above equation, we obtain$\angle \text{ DAL}=\arccos{\left(\dfrac{\sqrt5-1}{4}\right)}=72^\circ$
Now, triangles $\text{LAD}$ and $\text{DAK}$ are congruent. This is because $\text{LA = KA}$ (radii of [black] circle), $\text{AD = DA}$ (common side of both triangles) and $\text{DL = DK}$ (deduced above), so the triangles are congruent by the SSS theorem. In particular, this means that$\angle\text{ DAK}=\angle\text{ DAL}=72^\circ$
 I then considered triangle $\text {ALK.}$
I then considered triangle $\text {ALK.}$$\angle\text{ LAK}=\angle\text{ DAL}+\angle\text{ DAK}=144^\circ$
From the cosine rule, we can find the length of $\text{LK}:$
$\text{LK}=\sqrt{\text{LA}^2+\text{KA}^2-2\left(\text{LA}\right)\left(\text{KA}\right)\cos{\left(\angle \text{ LAK}\right)}}$
$\text{LA = KA}=1,$ since they are the radii of the circle $C_1$ (black), and we know that $\cos{\angle\text {LAK}}=\cos{144^\circ}=\frac{-1-\sqrt5}4.$ Substituting these values into the above equation, we obtain
$\text{LK}=\dfrac{\sqrt{10+2\sqrt5}}{2}$
So $\text{LK = DI = DJ.}$ We see then that triangle $\text{ALK}$ is congruent to triangles $\text{DAI}$ and $\text{DAJ}$ by the SSS theorem, since one side of one triangle is equal to another side of the other two triangles ($\text{LK = DI = DJ}$), and the other two sides of one triangle are equal to the other two sides of the other two triangles, because they are all radii of the circle $C_1$ (black).
In particular then, $\angle\text{ DAJ}=\angle\text{ DAI}=144^\circ.$ Also,
$\angle\text{ JAI}=360^\circ-\left(\angle\text{ DAJ}+\angle\text{ DAI}\right)$
So $\angle\text{ JAI}=72^\circ.$
Now, $\angle\text{ LAI}=\angle\text{ DAI}-\angle\text{ DAL}=72^\circ.$ Therefore, $\angle \text { KAJ}=360^\circ-\left(\angle \text{ DAK}+\angle \text{ DAL}+\angle \text{ LAI}+\angle \text{ JAI}\right)=72^\circ.$
Therefore, by the SAS congruence axiom, the triangles $\text{AIJ, AJK, AKD, ADL, ALI}$ are all congruent to each other and, in particular, $\text{IJ = JK = KD = DL = LI}$ and all the angles in one of the above triangles are equal to the angles in the corresponding four triangles, therefore $\angle\text{ I}=\angle\text{ J}=\angle\text{ K}=\angle\text{ D}=\angle\text{ L},$ where these angles are the interior angles of the shape $\text{IJKDL,}$ making this shape a regular pentagon.
It is also possible to prove that the construction gives a pentagon using coordinate geometry:
Using Cartesian coordinates with $A$ as the origin and $B$ at $(1,0)$.
Then, $D$ is at $(0,1)$, since it is the same distance away from $A$ as $B$ is but on a perpendicular line. $F$ is the midpoint of $AB$, so is at $(\frac 12,0)$.
Pythagoras' Theorem tells us that the distance $DF = \sqrt{1^2 + (\frac 12)^2} = \frac{\sqrt{5}}{2}$. Therefore $G$ is at $(\frac{1+\sqrt 5}2,0)$ and $H$ is at $(\frac{1-\sqrt 5}2,0)$.
Then, $DG = \sqrt{1^2 + \left( \frac{1+\sqrt 5}2 \right)^2} = \sqrt{1+\frac{6+2\sqrt 5}{4}} = \frac{\sqrt{10+2\sqrt{5}}}{2}$.
Then, looking at the equations of the two circles (black and yellow), we have:
\begin{eqnarray}
x^2 + y^2 &=& 1\\
x^2 + (y-1)^2 &=& \frac{5+\sqrt 5}2 \\
\end{eqnarray}
Subtracting one from the other yields:$$\begin{eqnarray}
y^2-(y-1)^2&=&1-\frac{5+\sqrt 5}{2}\\
\Rightarrow y^2-\left(y^2-2y+1\right) &=&1-\frac{5+\sqrt 5}{2}\\
\Rightarrow 2y-1 &=& 1-\frac{5+\sqrt 5}{2}\end{eqnarray}$$This has solution:$$y = -\frac{1+\sqrt 5}{2} = \cos 144^\circ$$
So $x =\pm \sin 144^\circ$, since $\left( \pm\sin 144^\circ \right) ^2 + \cos ^2 144^\circ = 1$
To use right-angled triangles, use the sine and cosine graphs to see how $\sin 144^\circ$ and $\cos 144^\circ$ compare to angles less than $90^\circ$:
$\sin 144^\circ = \sin (90^\circ-(144^\circ-90^\circ)) = \sin 36^\circ,\cos 144^\circ = -\cos(180^\circ-144^\circ)=-\cos36^\circ$
So the points $I$ and $J$ can be plotted as shown:

Meanwhile, $DH = \sqrt{1^2 + \left( \frac{1-\sqrt 5}2 \right)^2} = \sqrt{1+\frac{6-2\sqrt 5}{4}} = \frac{\sqrt{10-2\sqrt{5}}}{2}$.
Then, looking at the equations of the two circles, we have:
\begin{eqnarray}
x^2 + y^2 &=& 1\\
x^2 + (y-1)^2 &=& \frac{5-\sqrt 5}2 \\
\end{eqnarray}
Subtracting one from the other yields:$$2y-1 = 1-\frac{5-\sqrt 5}{2}$$This has solution:$$y = \frac{\sqrt 5-1}{2} = \cos 72^\circ$$
So $x =\pm \sin 72^\circ$, since $\left( \pm\sin 72^\circ \right) ^2 + \cos ^2 72^\circ = 1$
So the points $K$ and $L$ can be plotted as shown:

The shape $DLJIK$ is made up of five congruent isosceles triangles, so it is a regular pentagon.

