Name That Graph

This resource is from Underground Mathematics.
 

Sameer from Hymers College in the UK described a method for finding the equation of the curves:

Just from looking at the graph I know it is a quadratic graph, this means it contains an $x^2.$ The two forms of this [equation] are expanded and factorised.

An expanded formula looks like this: $y = x^2 -3x -4$

However solving a quadratic graph requires the factorised formula.

In order to factorise an equation, you need to look for two numbers.

In the equation $x^2 -3x - 4 = 0,$ the two numbers must add together to form $-3$ and multiply together to form $-4.$ These numbers are $1$ and $-4.$

The equation will look like this: $(x+1)(x-4) = 0.$

It has two solutions, this is because one of the brackets must equal $0.$

$x + 1 = 0$ or $x - 4 =0$   $\Rightarrow$   $x = -1$ or $x = 4$

Therefore $y=0$ when  $x = -1$ or $x = 4,$ so the graph passes through $-1$ and $4$ on the x axis. These are the roots.

Sameer and Sam from England used this idea to find the equation of the first graph. Sam wrote:

The curve crosses the x axis at $3$ and $-1.$ So $x= -1,3.$ $(x+1)(x-3)$ because at least one of the brackets has to equal $0.$ When you multiply out the brackets you get the equation [$y=$]$x^2-2x-3.$

Sergio from Kings College Alicante in Spain used another method to check this answer:

This is Sergio's work for the second graph:

Anna got a different equation for the second graph. Anna's method is similar to the method Sergio used to check the equation of the first graph. Here is Anna's work:

The minimum point of the graph is when $x=2,$ therefore $y=a(x-2)^2+k.$

$y=-4$ when $x=2$ therefore $k=-4.$

When $x=0,$ $y=8$ because the y-intercept is $8.$ Therefore $8=a\times(-2)^2-4 = 4a-4$ and so $a=3.$

So the equation is $y=3(x-2)^2-4.$

Check when $y=0:$

$\begin{align}3(x-2)^2-4&=0 \\ 3(x-2)^2 &= 4\\ (x-2)^2 &= \dfrac43 \\ x-2&=\pm\dfrac{2}{\sqrt3} \\ x&=2\pm\dfrac{2}{\sqrt3}\end{align}$

$2+\dfrac{2}{\sqrt3}\approx3.15$ and $2-\dfrac{2}{\sqrt3}\approx0.85$ which looks about right.

Can you see why Anna and Sergio got different answers? Whose answer do you think is right?

This is Sameer's work for the third graph:

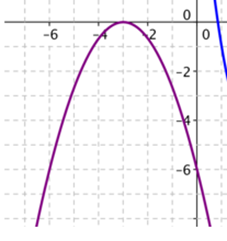
In this graph, the line is upside down compared to the others; this is because the $x^2$ is negative. The root is $-3,$ so the only solution is $-3.$

   $x = -3$   or    $x = -3$

$x + 3 = 0 or x + 3 = 0$

$(x+3)(x+3) = 0$

However, the $x^2$ is negative so one $x$ needs to be negative. This has to be the $x$ in the bracket with a $3$ so that the $3$ also becomes negative.

$-(x+3)(x+3) = 0.$

The expanded form is $-x^2 -6x -9$

Sergio added:

We need a y-intercept at $-6,$ not at $-9,$ so we multiply everything by $\dfrac{-6}{-9}=\dfrac23$:

$y=-\frac23x^2 -4x -6$