Inspecting Identities

This resource is from Underground Mathematics.
 

Gururvignesh from Hymers College in the UK sent in this solution:

1. We expand $\sin^2\frac x2$ and $\cos^2\frac x2$ so that it equals $\frac12(1-\cos x)$ and $\frac12(1+\cos x)$ respectively

2. We find out the amplitude, period, vertical shift and face shift by substituting the equation $y=a\cos(bx+c)+k$ into the expanded identity.

3. After finding the important points we can sketch the cos or sine graph and label the points.

$y=a\cos(bx+c)+k$

$a$ = amplitude (the height of the graph)

$b$ = period (how long it takes for the graph to repeat)

$c$ = period shift/phase shift

$k$ = vertical shift

$\cos^2\frac x2 = \frac12(1+\cos x)$

$\sin^2\frac x2= \frac12(1-\cos x)$

$\begin{split}y&=\cos^2\tfrac x2\\ &= \frac12+\frac{\cos x}2\end{split}$

$a=\frac12$

period = $\frac{2\pi}b = \frac{2\pi}1=2\pi$

vertical shift = $\frac12$

period shift = $0$

$y = \sin^2\frac x2$

$y =\frac12(1-\cos x)$

$a = -\frac12$ (which means the graph of cosine has to be flipped.)

period = $\frac{2\pi}b = \frac{2\pi}1=2\pi$

vertical shift = $\frac12$

period shift = $0$

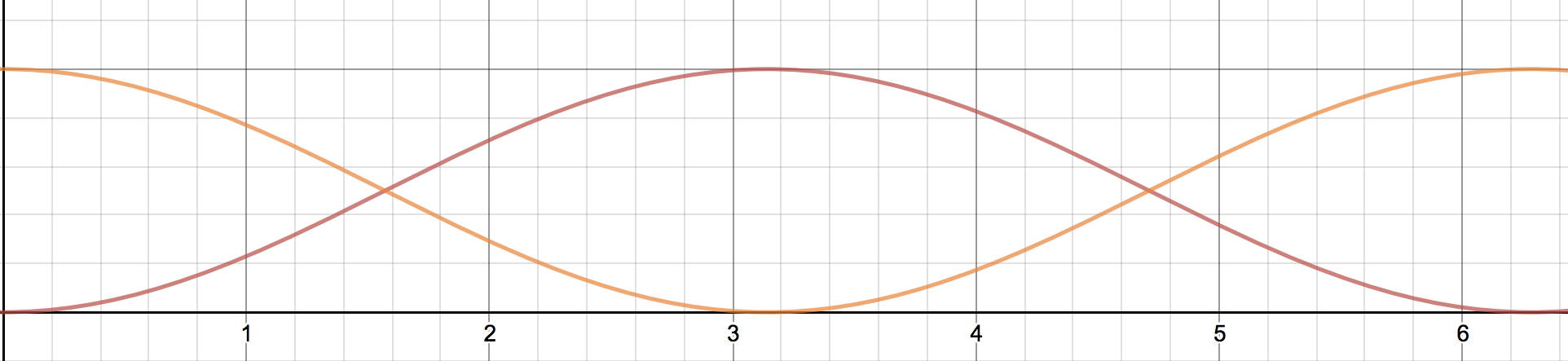
Click here to see a larger image.

The orange graph represents $y= \cos^2 \frac x2$

the red graph represents $y= \sin^2 \frac x2$