t for tan
If we write t = \tan \theta, then the following equations are true.
\begin{align*}
\tan(2\theta) &= \frac{2t}{1-t^2}, \\
\sin(2\theta) &= \frac{2t}{1+t^2}, \\
\cos(2\theta) &= \frac{1-t^2}{1+t^2}.
\end{align*}
Can you use this diagram to obtain these formulae?
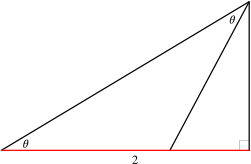
For what range of values of \theta does this argument work?
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
You may also like
Powerful Quadratics
This comes in two parts, with the first being less fiendish than the second. It’s great for practising both quadratics and laws of indices, and you can get a lot from making sure that you find all the solutions. For a real challenge (requiring a bit more knowledge), you could consider finding the complex solutions.
Discriminating
You're invited to decide whether statements about the number of solutions of a quadratic equation are always, sometimes or never true.
Factorisable Quadratics
This will encourage you to think about whether all quadratics can be factorised and to develop a better understanding of the effect that changing the coefficients has on the factorised form.