Skip over navigation
Each time you have a game, you add up the score of the three darts.
Your challenge is to have four games each with the same total score, but made in different ways.
However, note that 1 and 2 on the left target and 3 on the right target is the same as 1 on the left target and 2 and 3 on the right target, so is counted as just one solution.
Have three games. The three totals must give three consecutive numbers.
In the nine darts used no number must occur more than twice.
So, when Raj chooses:
Game 1: 2 + 3 + 4 = 9
Game 2: 1 + 4 + 5 = 10
Game 3: 1 + 5 + 5 = 11
This is NOT allowed as three 5s have been used and the maximum is two.
You now move on to having three targets with four darts for each game.
As before you can only have one dart in any coloured sector of a target.
The targets are:
1, 2, 3
1, 2, 3, 4
1, 2, 3, 4, 5.
Firstly see how many different totals you can make.
Finally find all the ways of getting the set of three consecutive 11, 12, 13
But in a set of three answers you must not use the same number more than three times.
So, when Sara chooses:
Game 1 1 + 2 + 3 + 5 = 11
Game 2 1 + 2 + 4 + 5 = 12
Game 3 2 + 2 + 4 + 5 = 13
This is not allowed as four 2s have been used and the maximum is three.
Find as many answers as you can.



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Dart Target
Age 7 to 11
Challenge Level 





We have two different targets and a set of three darts.
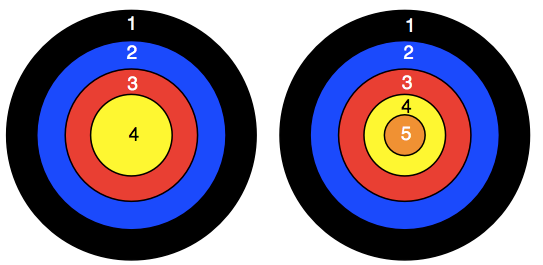



You use three darts for each game. All the darts always hit the target.
An Important Rule:-
You can only have one dart in the same coloured area on any one target, but you could, for example, have a dart in red 3 on the left target and another dart in red 3 on the right target.
CHALLENGE 1
Each time you have a game, you add up the score of the three darts.
Your challenge is to have four games each with the same total score, but made in different ways.
However, note that 1 and 2 on the left target and 3 on the right target is the same as 1 on the left target and 2 and 3 on the right target, so is counted as just one solution.
CHALLENGE 2
Have three games. The three totals must give three consecutive numbers.
In the nine darts used no number must occur more than twice.
So, when Raj chooses:
Game 1: 2 + 3 + 4 = 9
Game 2: 1 + 4 + 5 = 10
Game 3: 1 + 5 + 5 = 11
This is NOT allowed as three 5s have been used and the maximum is two.
CHALLENGE 3
You now move on to having three targets with four darts for each game.
As before you can only have one dart in any coloured sector of a target.
The targets are:
1, 2, 3
1, 2, 3, 4
1, 2, 3, 4, 5.
Firstly see how many different totals you can make.
Finally find all the ways of getting the set of three consecutive 11, 12, 13
But in a set of three answers you must not use the same number more than three times.
So, when Sara chooses:
Game 1 1 + 2 + 3 + 5 = 11
Game 2 1 + 2 + 4 + 5 = 12
Game 3 2 + 2 + 4 + 5 = 13
This is not allowed as four 2s have been used and the maximum is three.
Find as many answers as you can.
You may also like
Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.

