Painting Possibilities
We have an open-topped multicoloured box on the left with four coloured cubes waiting to go in (labelled A in the picture below).
Only the outside has been painted, not the base, nor the inside.
Each of the four separate cubes has been painted all over.
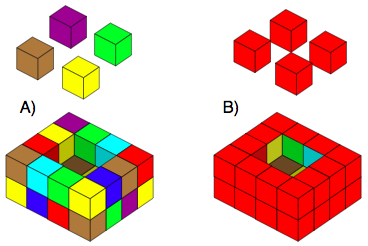
The box always has walls and base that are just 1 cube thick.
Covering one face of a little cube uses 1 unit of paint.
CHALLENGE 1
How many units of paint have been used to turn the muliticoloured box (A) into the painted box (B)?
How many units of paint have been used to cover the four cubes that fit in the box?
Here is another example which would need twelve little cubes to fill the open box (labelled as C):
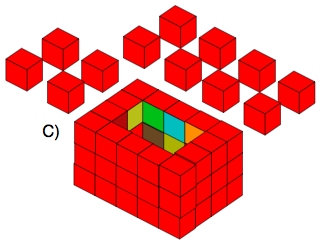
Similarly how many units of paint have been used for the outside of the box?
How many units of paint have been used to cover the twelve cubes which fit inside it?
Do either of these two boxes use the same amount of paint as the cubes that would fill them?
CHALLENGE 2
Find the size of an open box that needs the same amount of paint to cover the cubes that fill it as its outside.
CHALLENGE 3
In diagram B, the number of units of paint needed to cover the box is 20 more than the number needed to cover the four cubes that fill the box.
Can you find some more open boxes which use 20 more units of paint to cover their outsides than to cover the cubes that fill them?
You may also like
Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.