Skip over navigation
(Note that although they are all called 'open squares' the first two are not actually open, but we will still use them in these challenges.)
What would the next five open squares look like?
How many small cubes would each one use?
We now stack the open squares up to make hollow pyramids, each open square resting on the one that is the next size bigger.
We can use just the first six hollow pyramids. Here are the first five, you will also need to consider the sixth:
This time your challenge is to use one, two, three or four hollow pyramids and to find the total number of cubes used. However, you cannot use two of the same pyramid in any total.
Can you find a way to make all totals up to and including 59 small cubes?
If there are some totals you cannot make, can you explain why?
Open Squares
Age 7 to 11
Challenge Level 
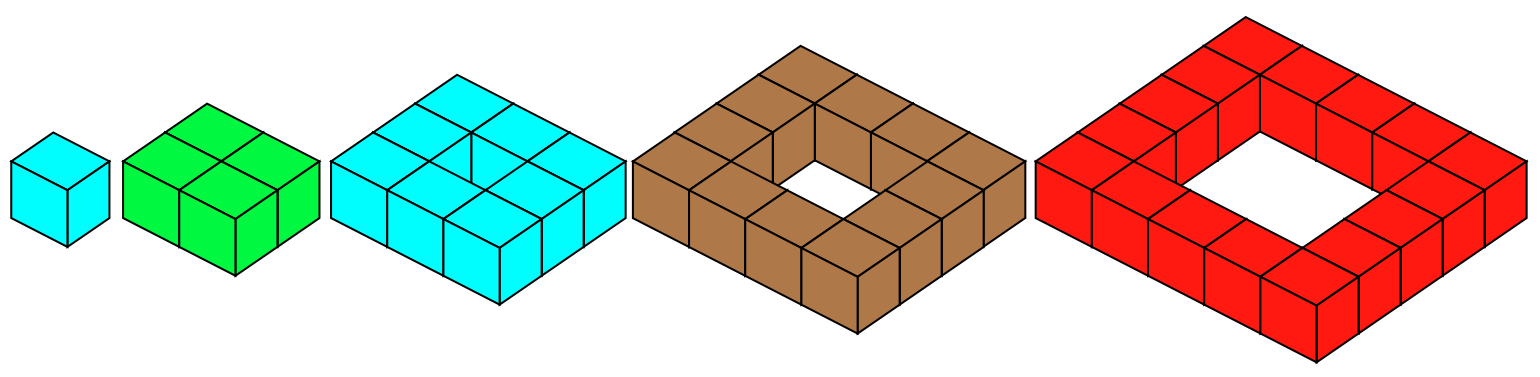
For these challenges, we are going to find the total number of small cubes used to make different models that we will call open squares.
Here are the first five open squares:
Here are the first five open squares:
(Note that although they are all called 'open squares' the first two are not actually open, but we will still use them in these challenges.)
What would the next five open squares look like?
How many small cubes would each one use?
CHALLENGE 1
Using two, three or four of the first ten open squares, your challenge is to make totals (of little cubes) between 50 and 60 (not including 50 or 60).
You can only use one of any size open square in each total you make, for example 16 + 36 = 52 is right but 4 + 4 + 8 + 36 = 52 is not allowed because it used two 4s.
If there are some totals between 50 and 60 you cannot make, explain why that is so.
You can only use one of any size open square in each total you make, for example 16 + 36 = 52 is right but 4 + 4 + 8 + 36 = 52 is not allowed because it used two 4s.
If there are some totals between 50 and 60 you cannot make, explain why that is so.
CHALLENGE 2
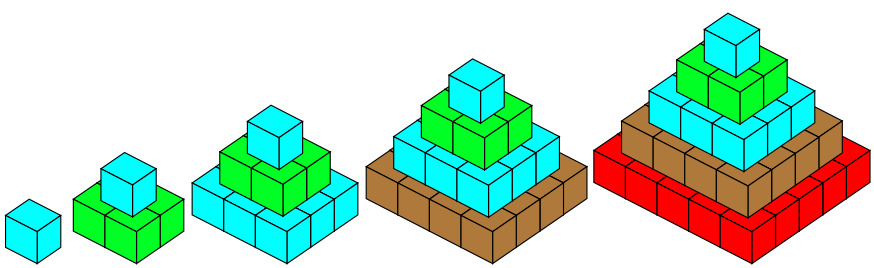
We now stack the open squares up to make hollow pyramids, each open square resting on the one that is the next size bigger.
We can use just the first six hollow pyramids. Here are the first five, you will also need to consider the sixth:
This time your challenge is to use one, two, three or four hollow pyramids and to find the total number of cubes used. However, you cannot use two of the same pyramid in any total.
Can you find a way to make all totals up to and including 59 small cubes?
If there are some totals you cannot make, can you explain why?
You may also like
Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.