Skip over navigation

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Cuboid Faces
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Working out the lengths of the edges
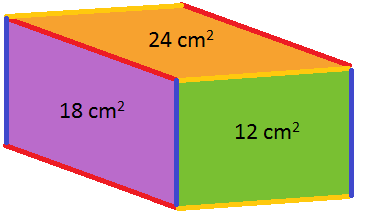
From this diagram, we can see that:
If the yellow edge is 6 cm long and the blue edge is 2 cm long, then the red edge must be 9 cm long, because 2$\times$9 = 18. However, then the orange face would have area 6$\times$9 = 54 square centimetres, which is not right.
If the yellow edge is 2 cm long and the blue edge is 6 cm long, then the red edge must be 3 cm long, because 6$\times$3 = 18. However, then the orange face would have area 2$\times$3 = 6 square centimetres, which is not right.
If the yellow edge is 4 cm long and the blue edge is 3 cm long, then the red edge must be 6 cm long, because 3$\times$6 = 18. Then the orange face would have area 4$\times$6 = 24 square centimetres, which is right.
So the edges of the cuboid are 3 cm, 4 cm and 6 cm long, which means the volume of the cuboid is 3$\times$4$\times$6 = 72 cm$^3$.
Using algebra to find the lengths of the edges
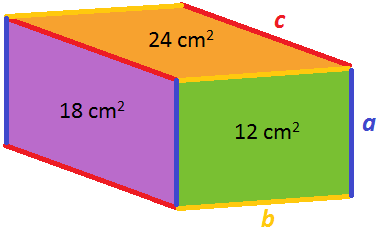
If we call the lengths of the edges $a$, $b$ and $c$, then $ab=12$, $ac=18$ and $bc=24$.
From here, we can use a trial approach to work out $a$, $b$ and $c$ similar to the method described above, or we can solve these equations, as shown below.
Since $ab=12$, we can say that $a=\dfrac{12}{b}$.
Substituting into $ac=18$, we get $\dfrac{12}{b}\times c=18$. Rearranging, $12c=18b$, so $c=\dfrac{18b}{12}=\dfrac{3b}{2}$.
Substituting into $bc=24$ now gives $b\times\dfrac{3b}{2}=24$, so $\dfrac{3b^{2}}{2}=24$, so $b^{2}=16$, so $b=4$.
So $a=\dfrac{12}{4}=3$ and $c=\dfrac{3\times4}{2}=6$.
So the volume, given by $abc$, is equal to $3\times4\times6=72$ cm$^3$.
Using algebra to find the volume directly
As in the picture above, we can call the lengths of the edges $a$, $b$ and $c$. So $ab=12$, $ac=18$ and $bc=24$.
We want the volume of the cuboid, $V=abc$.
Notice that $ab\times ac\times bc=a^2b^2c^2=(abc)^2=V^2$.
So $12\times18\times24=V^2$.
So $V=\sqrt{12\times18\times24}=72$.
So the volume is $72$ cm$^3$.

From this diagram, we can see that:
- the length of the yellow edge multiplied by the length of the blue edge must be 12
- the length of the red edge multiplied by the length of the blue edge must be 18
- the length of the yellow edge multiplied by the length of the red edge must be 24.
If the yellow edge is 6 cm long and the blue edge is 2 cm long, then the red edge must be 9 cm long, because 2$\times$9 = 18. However, then the orange face would have area 6$\times$9 = 54 square centimetres, which is not right.
If the yellow edge is 2 cm long and the blue edge is 6 cm long, then the red edge must be 3 cm long, because 6$\times$3 = 18. However, then the orange face would have area 2$\times$3 = 6 square centimetres, which is not right.
If the yellow edge is 4 cm long and the blue edge is 3 cm long, then the red edge must be 6 cm long, because 3$\times$6 = 18. Then the orange face would have area 4$\times$6 = 24 square centimetres, which is right.
So the edges of the cuboid are 3 cm, 4 cm and 6 cm long, which means the volume of the cuboid is 3$\times$4$\times$6 = 72 cm$^3$.
Using algebra to find the lengths of the edges

If we call the lengths of the edges $a$, $b$ and $c$, then $ab=12$, $ac=18$ and $bc=24$.
From here, we can use a trial approach to work out $a$, $b$ and $c$ similar to the method described above, or we can solve these equations, as shown below.
Since $ab=12$, we can say that $a=\dfrac{12}{b}$.
Substituting into $ac=18$, we get $\dfrac{12}{b}\times c=18$. Rearranging, $12c=18b$, so $c=\dfrac{18b}{12}=\dfrac{3b}{2}$.
Substituting into $bc=24$ now gives $b\times\dfrac{3b}{2}=24$, so $\dfrac{3b^{2}}{2}=24$, so $b^{2}=16$, so $b=4$.
So $a=\dfrac{12}{4}=3$ and $c=\dfrac{3\times4}{2}=6$.
So the volume, given by $abc$, is equal to $3\times4\times6=72$ cm$^3$.
Using algebra to find the volume directly
As in the picture above, we can call the lengths of the edges $a$, $b$ and $c$. So $ab=12$, $ac=18$ and $bc=24$.
We want the volume of the cuboid, $V=abc$.
Notice that $ab\times ac\times bc=a^2b^2c^2=(abc)^2=V^2$.
So $12\times18\times24=V^2$.
So $V=\sqrt{12\times18\times24}=72$.
So the volume is $72$ cm$^3$.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Hallway Borders
What are the possible dimensions of a rectangular hallway if the number of tiles around the perimeter is exactly half the total number of tiles?

