Skip over navigation
Rotating the hexagon and using a different triangle
In the diagram below, the hexagon has ben rotated so that the base of the triangle is horzontal. The isosceles triangle outlined and the grey triangle have the same base and height, so they have the same area.
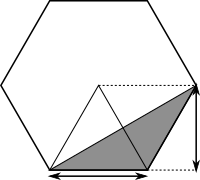
Using the symmetry of the regular hexagon, it can be split into $6$ of these triangles, as shown below. So the area of the triangle is equal to $\frac{1}{6}$ of the area of the hexagon, which is $\frac{1}{6}$ of $48$ m$^2,$ which is $8$ m$^2.$
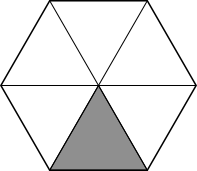
Splitting the hexagon into smaller shapes
Using the symmetry of the regular hexagon, we can split it into triangles or rhombuses:
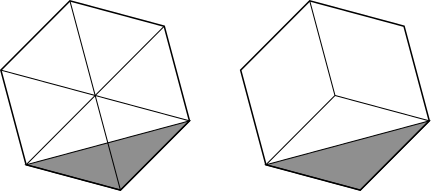
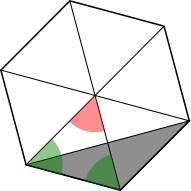
Using triangles, the red angle is $\frac{1}{6}$ of $360^\text{o},$ which is $60^\text{o},$ because it is $\frac{1}{6}$ of the circle at the centre of the hexagon.
The triangle is isosceles, so the two green angles are equal, and they add up to $120^\text{o},$ since all of the angles in a triangle add up to $180^\text{o}.$ So they are also $60^\text{o},$ so the triangles are equilateral.
Notice now that the boundary of the grey area is a line of symmetry of the two bottom triangles. So the grey area is the same as the area of two half-triangles, which is the same as one whole triangle.
So the grey area is $\frac{1}{6}$ of the area of the hexagon, which is $\frac{1}{6}$ of $48$ m$^2,$ which is $8$ m$^2.$
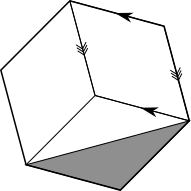 Using rhombuses, the sides marked as parallel must be parallel. This is because the lines used to split the hexagon into diamonds must be along lines of symmetry of the hexagon.
Using rhombuses, the sides marked as parallel must be parallel. This is because the lines used to split the hexagon into diamonds must be along lines of symmetry of the hexagon.
This means the quadrilaterals must be parallelograms, and so they must be rhombuses, since all of the sides of the hexagon are equal.
So the rhombuses are symmetrical and the boundary of the grey area is a line of symmetry of the bottom rhombus. So the grey area is the same as the area of half a rhombus, which is is $\frac{1}{6}$ of the area of the hexagon, which is $\frac{1}{6}$ of $48$ m$^2,$ which is $8$ m$^2.$
Using trigonometry
The interior angle of a hexagon is $120^\text{o}$ (there are various ways to show this, including using the diagram above, or splitting the hexagon into triangles and counting angles, or using exterior angles), which is shown on the diagram below.
Finding the areas of the 3 shapes on the diagram below in terms of the side length $s$ will allow us to find the $s$ and therefore the shaded area.

Using the formula for the area of a triangle $A=\frac{1}{2}ab\sin{C},$ the area of the shaded triangle is $\frac{1}{2}s^2\sin{120}=\frac{1}{4}s^2\sqrt{3}$ m$^2.$
The area of the green triangle is also $\frac{1}{4}s^2\sqrt{3}$ m$^2.$ The area of the rectangle is $as$ m$^2,$ where we can find $a$ using the cosine rule:$$\begin{align}&a^2=s^2+s^2-2\times s\times s \cos{120}\\
\Rightarrow&a^2=2s^2-s^2\cos{120}\\
\Rightarrow&a^2=3s^2\\
\Rightarrow&a=\sqrt{3s^2}=s\sqrt{3}\end{align}$$ So the area of the rectangle is $s\sqrt{3}\times s = s^2\sqrt{3}$ m$^2.$
That is four times the area of the shaded triangle, since $4\times\frac{1}{4}s^2\sqrt{3}=s^2\sqrt{3}.$ So the shaded triangle fits into the hexagon $2+4=6$ times - so it occupies $\frac{1}{6}$ of the total area of the hexagon. So its area is $\frac{1}{6}$ of $48$ m$^2,$ which is $8$ m$^2.$

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Triangle in the Corner
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Rotating the hexagon and using a different triangle
In the diagram below, the hexagon has ben rotated so that the base of the triangle is horzontal. The isosceles triangle outlined and the grey triangle have the same base and height, so they have the same area.

Using the symmetry of the regular hexagon, it can be split into $6$ of these triangles, as shown below. So the area of the triangle is equal to $\frac{1}{6}$ of the area of the hexagon, which is $\frac{1}{6}$ of $48$ m$^2,$ which is $8$ m$^2.$

Splitting the hexagon into smaller shapes
Using the symmetry of the regular hexagon, we can split it into triangles or rhombuses:


Using triangles, the red angle is $\frac{1}{6}$ of $360^\text{o},$ which is $60^\text{o},$ because it is $\frac{1}{6}$ of the circle at the centre of the hexagon.
The triangle is isosceles, so the two green angles are equal, and they add up to $120^\text{o},$ since all of the angles in a triangle add up to $180^\text{o}.$ So they are also $60^\text{o},$ so the triangles are equilateral.
Notice now that the boundary of the grey area is a line of symmetry of the two bottom triangles. So the grey area is the same as the area of two half-triangles, which is the same as one whole triangle.
So the grey area is $\frac{1}{6}$ of the area of the hexagon, which is $\frac{1}{6}$ of $48$ m$^2,$ which is $8$ m$^2.$
 Using rhombuses, the sides marked as parallel must be parallel. This is because the lines used to split the hexagon into diamonds must be along lines of symmetry of the hexagon.
Using rhombuses, the sides marked as parallel must be parallel. This is because the lines used to split the hexagon into diamonds must be along lines of symmetry of the hexagon.This means the quadrilaterals must be parallelograms, and so they must be rhombuses, since all of the sides of the hexagon are equal.
So the rhombuses are symmetrical and the boundary of the grey area is a line of symmetry of the bottom rhombus. So the grey area is the same as the area of half a rhombus, which is is $\frac{1}{6}$ of the area of the hexagon, which is $\frac{1}{6}$ of $48$ m$^2,$ which is $8$ m$^2.$
Using trigonometry
The interior angle of a hexagon is $120^\text{o}$ (there are various ways to show this, including using the diagram above, or splitting the hexagon into triangles and counting angles, or using exterior angles), which is shown on the diagram below.
Finding the areas of the 3 shapes on the diagram below in terms of the side length $s$ will allow us to find the $s$ and therefore the shaded area.

Using the formula for the area of a triangle $A=\frac{1}{2}ab\sin{C},$ the area of the shaded triangle is $\frac{1}{2}s^2\sin{120}=\frac{1}{4}s^2\sqrt{3}$ m$^2.$
The area of the green triangle is also $\frac{1}{4}s^2\sqrt{3}$ m$^2.$ The area of the rectangle is $as$ m$^2,$ where we can find $a$ using the cosine rule:$$\begin{align}&a^2=s^2+s^2-2\times s\times s \cos{120}\\
\Rightarrow&a^2=2s^2-s^2\cos{120}\\
\Rightarrow&a^2=3s^2\\
\Rightarrow&a=\sqrt{3s^2}=s\sqrt{3}\end{align}$$ So the area of the rectangle is $s\sqrt{3}\times s = s^2\sqrt{3}$ m$^2.$
That is four times the area of the shaded triangle, since $4\times\frac{1}{4}s^2\sqrt{3}=s^2\sqrt{3}.$ So the shaded triangle fits into the hexagon $2+4=6$ times - so it occupies $\frac{1}{6}$ of the total area of the hexagon. So its area is $\frac{1}{6}$ of $48$ m$^2,$ which is $8$ m$^2.$
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Hallway Borders
What are the possible dimensions of a rectangular hallway if the number of tiles around the perimeter is exactly half the total number of tiles?

