Skip over navigation
Answer: 14
Balancing numbers at each end
Adding from 1 will be the same as adding from 20
Use up the large numbers by balancing them with little numbers
$20=4\times5$ so use $4$ numbers close to $5$ to make $20$:
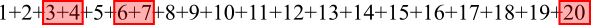
$19=9+10$
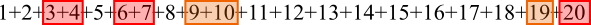
$18=5+2+11$
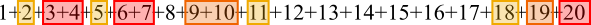
There aren't enough small numbers to make $17$ so take $16$ and $17$ together $=33$
Use up the $8:\ \ \ 33-8=25=12+13$

Which leaves $14+1=15$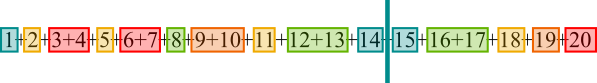
So the sum from $1$ to $14$ is the same as the sum from $15$ to $20$.
Adding up all of the numbers
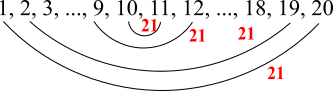
10 pairs of numbers which add up to 21
$\therefore$ sum of all 20 = 10$\times$21 = 210
Each sum is equal to 210$\div$2 = 105
Add up until 105 - quicker using larger numbers
20 + 20 + 20 + 20 + 20 = 5 less than 105
20 + 19 + 18 + 17 + 16 = 5 + 1 + 2 + 3 + 4 less than 105 = 15 less than 105
20 + 19 + ... + 15 = 105
$n$ is 14
Comparing Milly's sum to $1+2+3+4+...+20$
Milly's and Billy's sums are equal and add up to $1+2+3+4+...+20$, so Milly's sum must be equal to half of $1+2+3+4+...+20.$
So $$\begin{split}1+2+3+4+...+n&=\dfrac{1+2+3+4+...+20}{2}\\&=\tfrac{1}{2}+\tfrac{2}{2}+\tfrac{3}{2}+\tfrac{4}{2}+...+\tfrac{20}{2}\\
&=\tfrac{1}{2}+1+1\tfrac{1}{2}+2+...+10\end{split}$$
Rewriting the right hand side to put the integers first, we can begin to subtract numbers from both sides:
$$\begin{align}1+2+3+4+...+10+&11+...+n=1+2+3+...+10+\tfrac{1}{2}+1\tfrac{1}{2}+2\tfrac{1}{2}+...+9\tfrac{1}{2}\\\Rightarrow &11+...+n=\tfrac{1}{2}+1\tfrac{1}{2}+...+9\tfrac{1}{2}\end{align}$$
Now, looking at the right hand side, $1\frac{1}{2}+9\frac{1}{2}=11$, so we can remove 11 from both sides of the equation:
$$12+...+n=\frac{1}{2}+2\frac{1}{2}+3\frac{1}{2}+4\frac{1}{2}+5\frac{1}{2}+6\frac{1}{2}+7\frac{1}{2}+8\frac{1}{2}$$.
Similarly, $3\frac{1}{2}+8\frac{1}{2}=12$ and $5\frac{1}{2}+7\frac{1}{2}=13$.
Removing those from the left and right hand side just leaves
$\frac{1}{2}+2\frac{1}{2}+4\frac{1}{2}+6\frac{1}{2}$ on the right hand side, which is equal to $14,$
so $n=14.$
Using formulae
Using the formula that $1+2+3+...+r=\frac{1}{2}r(r+1)$ for any whole number $r$, Milly's sum is equal to $\frac{1}{2}n(n+1)$ and $1+2+3+...+20=\frac{1}{2}20(21)=210.$
Since Milly's and Billy's sums are equal and add up to $210$, Milly's sum must be equal to half of $210,$ so $\frac{1}{2}n(n+1)=105
\Rightarrow n(n+1)=210.$
From here, you could find $n$ using factorisation ($210=2\times3\times5\times7=14\times15$), or expand and solve the quadratic equation $n^2+n-210=0$
By factorisation
$(n-14)(n-15)=0\Rightarrow n=14$ or $n=-15,$ so $n=14$ since $n$ is positive.
Using the quadratic formula
Let $a=1,$ $b=1,$ $c=-210$ and $n=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$ $$\begin{align}n&=\dfrac{-1\pm\sqrt{1--4\times1\times210}}{2}\\&=\dfrac{-1\pm\sqrt{841}}{2}\\&\dfrac{-1\pm29}{2}\end{align}$$ Which gives $
n=14$ or $n=-15,$ so $n=14$ since $n$ is positive.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Comparing Totals
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Answer: 14
Balancing numbers at each end
Adding from 1 will be the same as adding from 20
Use up the large numbers by balancing them with little numbers
$20=4\times5$ so use $4$ numbers close to $5$ to make $20$:
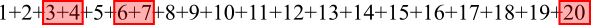
$19=9+10$
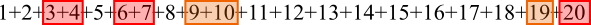
$18=5+2+11$
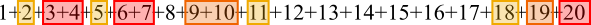
There aren't enough small numbers to make $17$ so take $16$ and $17$ together $=33$
Use up the $8:\ \ \ 33-8=25=12+13$

Which leaves $14+1=15$
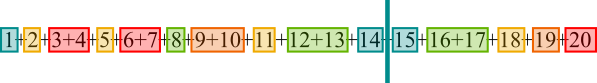
So the sum from $1$ to $14$ is the same as the sum from $15$ to $20$.
Adding up all of the numbers
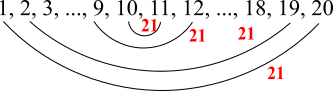
10 pairs of numbers which add up to 21
$\therefore$ sum of all 20 = 10$\times$21 = 210
Each sum is equal to 210$\div$2 = 105
Add up until 105 - quicker using larger numbers
20 + 20 + 20 + 20 + 20 = 5 less than 105
20 + 19 + 18 + 17 + 16 = 5 + 1 + 2 + 3 + 4 less than 105 = 15 less than 105
20 + 19 + ... + 15 = 105
$n$ is 14
Comparing Milly's sum to $1+2+3+4+...+20$
Milly's and Billy's sums are equal and add up to $1+2+3+4+...+20$, so Milly's sum must be equal to half of $1+2+3+4+...+20.$
So $$\begin{split}1+2+3+4+...+n&=\dfrac{1+2+3+4+...+20}{2}\\&=\tfrac{1}{2}+\tfrac{2}{2}+\tfrac{3}{2}+\tfrac{4}{2}+...+\tfrac{20}{2}\\
&=\tfrac{1}{2}+1+1\tfrac{1}{2}+2+...+10\end{split}$$
Rewriting the right hand side to put the integers first, we can begin to subtract numbers from both sides:
$$\begin{align}1+2+3+4+...+10+&11+...+n=1+2+3+...+10+\tfrac{1}{2}+1\tfrac{1}{2}+2\tfrac{1}{2}+...+9\tfrac{1}{2}\\\Rightarrow &11+...+n=\tfrac{1}{2}+1\tfrac{1}{2}+...+9\tfrac{1}{2}\end{align}$$
Now, looking at the right hand side, $1\frac{1}{2}+9\frac{1}{2}=11$, so we can remove 11 from both sides of the equation:
$$12+...+n=\frac{1}{2}+2\frac{1}{2}+3\frac{1}{2}+4\frac{1}{2}+5\frac{1}{2}+6\frac{1}{2}+7\frac{1}{2}+8\frac{1}{2}$$.
Similarly, $3\frac{1}{2}+8\frac{1}{2}=12$ and $5\frac{1}{2}+7\frac{1}{2}=13$.
Removing those from the left and right hand side just leaves
$\frac{1}{2}+2\frac{1}{2}+4\frac{1}{2}+6\frac{1}{2}$ on the right hand side, which is equal to $14,$
so $n=14.$
Using formulae
Using the formula that $1+2+3+...+r=\frac{1}{2}r(r+1)$ for any whole number $r$, Milly's sum is equal to $\frac{1}{2}n(n+1)$ and $1+2+3+...+20=\frac{1}{2}20(21)=210.$
Since Milly's and Billy's sums are equal and add up to $210$, Milly's sum must be equal to half of $210,$ so $\frac{1}{2}n(n+1)=105
\Rightarrow n(n+1)=210.$
From here, you could find $n$ using factorisation ($210=2\times3\times5\times7=14\times15$), or expand and solve the quadratic equation $n^2+n-210=0$
By factorisation
$(n-14)(n-15)=0\Rightarrow n=14$ or $n=-15,$ so $n=14$ since $n$ is positive.
Using the quadratic formula
Let $a=1,$ $b=1,$ $c=-210$ and $n=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$ $$\begin{align}n&=\dfrac{-1\pm\sqrt{1--4\times1\times210}}{2}\\&=\dfrac{-1\pm\sqrt{841}}{2}\\&\dfrac{-1\pm29}{2}\end{align}$$ Which gives $
n=14$ or $n=-15,$ so $n=14$ since $n$ is positive.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

