Skip over navigation
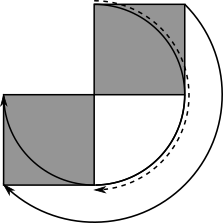
This diagram shows the paths of the three corners that are not the centre of rotation as the ink stamp is rotated.
”‹
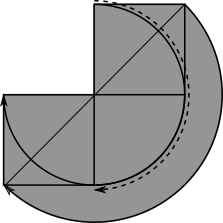
Everything within the large semicircle, or the beginning and ending positions of the stamp will be coloured black.
The radius of the semicircle is equal to the diagonal of the ink stamp.
Since the sides of the stamp are all $1$ cm, we can find the length of the diagonal using Pythagoras' Theorem: $1^2+1^2=r^2\Rightarrow 2=r^2\Rightarrow r=\sqrt{2}$ cm
The area of the semicircle is half of the area of a full circle of radius $\sqrt{2},$ so half of $\pi\sqrt{2}^2,$ which is half of $2\pi,$ which is $\pi$ cm$^2.$
The total area is the area of the semicircle plus the areas of the two half-squares that stick out above it. Each square has area $1$ cm$^2,$ so the two halves together have area $1$ cm$^2.$
So the total area is $(\pi+1)$ cm$^2.$
Coloured Black
Age 14 to 16
ShortChallenge Level 
This diagram shows the paths of the three corners that are not the centre of rotation as the ink stamp is rotated.
”‹Everything within the large semicircle, or the beginning and ending positions of the stamp will be coloured black.
The radius of the semicircle is equal to the diagonal of the ink stamp.
Since the sides of the stamp are all $1$ cm, we can find the length of the diagonal using Pythagoras' Theorem: $1^2+1^2=r^2\Rightarrow 2=r^2\Rightarrow r=\sqrt{2}$ cm
The area of the semicircle is half of the area of a full circle of radius $\sqrt{2},$ so half of $\pi\sqrt{2}^2,$ which is half of $2\pi,$ which is $\pi$ cm$^2.$
The total area is the area of the semicircle plus the areas of the two half-squares that stick out above it. Each square has area $1$ cm$^2,$ so the two halves together have area $1$ cm$^2.$
So the total area is $(\pi+1)$ cm$^2.$
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
A Problem of Time
Consider a watch face which has identical hands and identical marks for the hours. It is opposite to a mirror. When is the time as read direct and in the mirror exactly the same between 6 and 7?
Back in Time
How many times a day does a 24 hour digital clock look the same when reflected in a horizontal line?