Skip over navigation
Using the formula for internal angles of a polygon
The internal angles of an $n$ sided polygon sum to $(n-2) \times 180^\text{o}$, so for a hexagon the internal angles sum to $180(6 - 2)=720$ degrees.
The interior angles not shown are $360^\text{o}-75^\text{o}=285^\text{o}$ and $ (360 - x)^\text{o}$. So $$\begin{align}26+27+24+23+285+(360-x)&=720\\
\Rightarrow 385+360-x&=720\\
\Rightarrow 745-x&=720\\
\Rightarrow x&=25\end{align}$$
Using triangles inside the hexagon
Drawing lines from the vertex with the $x^\text{o}$ angle to the other vertices makes four triangles, A, B, C and D.
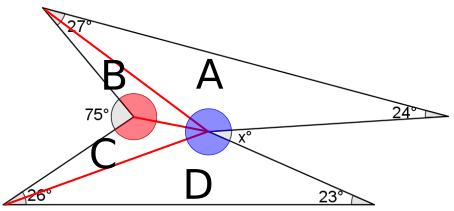
The sum of the angles in each of the triangles is $180^\text{o}$, so the sum of the angles in all four triangles is $180^\text{o}\times4=720^\text{o}$. So
The blue angle makes a full circle with the $x^\text{o}$ angle, so it must be $(360-x)^\text{o}$. This gives $$\begin{align}26+27+24+23+285+(360-x)&=720\\
\Rightarrow 385+360-x&=720\\
\Rightarrow 745-x&=720\\
\Rightarrow x&=25\end{align}$$
Using external angles on a diagram
Imagine starting at the $23^\text{o}$ angle and travelling to the left, and walking along the perimeter of the hexagon.
You would arrive at the $26^\text{o}$ angle and then need to rotate through the green angle shown to be facing in the correct direction to walk along the next side. The green angle is $154^\text{o}$ because $154 + 26 = 180.$
The full journey is shown on the diagram below. The two angles that are shown in red are red because the turn is the other way (anticlockwise, not clockwise).
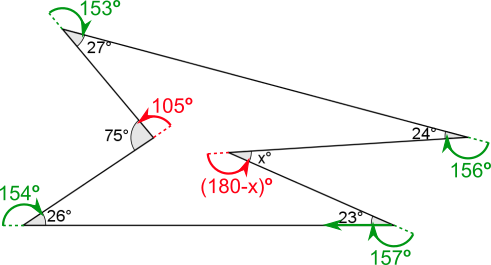
By the time you arrive back at the $23^\text{o}$ angle and rotate $153^\text{o}$, you are facing in the same direction you started in, so you have turned through a total of $360^\text{o}$.
You have also turned forwards through the green angles and backwards through the red angles, so the sum of the green angles subtract the sum of the red angles must be $360^\text{o}$. $$\begin{align}154 - 105 + 153 + 156 + -(180 - x ) + 157 &= 360\\
\Rightarrow 515-180+x&=360\\
\Rightarrow 515+x&=540\\
\Rightarrow x&=25\end{align}$$


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Funky Hexagon
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Using the formula for internal angles of a polygon
The internal angles of an $n$ sided polygon sum to $(n-2) \times 180^\text{o}$, so for a hexagon the internal angles sum to $180(6 - 2)=720$ degrees.
The interior angles not shown are $360^\text{o}-75^\text{o}=285^\text{o}$ and $ (360 - x)^\text{o}$. So $$\begin{align}26+27+24+23+285+(360-x)&=720\\
\Rightarrow 385+360-x&=720\\
\Rightarrow 745-x&=720\\
\Rightarrow x&=25\end{align}$$
Using triangles inside the hexagon
Drawing lines from the vertex with the $x^\text{o}$ angle to the other vertices makes four triangles, A, B, C and D.

The sum of the angles in each of the triangles is $180^\text{o}$, so the sum of the angles in all four triangles is $180^\text{o}\times4=720^\text{o}$. So
$26+27+24+23+$ the red angle $+$ the blue angle $=720$
The red angle makes a full circle with the $75^\text{o}$ angle, so it must be $360^\text{o}-75^\text{o}=285^\text{o}$.The blue angle makes a full circle with the $x^\text{o}$ angle, so it must be $(360-x)^\text{o}$. This gives $$\begin{align}26+27+24+23+285+(360-x)&=720\\
\Rightarrow 385+360-x&=720\\
\Rightarrow 745-x&=720\\
\Rightarrow x&=25\end{align}$$
Using external angles on a diagram
Imagine starting at the $23^\text{o}$ angle and travelling to the left, and walking along the perimeter of the hexagon.
You would arrive at the $26^\text{o}$ angle and then need to rotate through the green angle shown to be facing in the correct direction to walk along the next side. The green angle is $154^\text{o}$ because $154 + 26 = 180.$
The full journey is shown on the diagram below. The two angles that are shown in red are red because the turn is the other way (anticlockwise, not clockwise).

By the time you arrive back at the $23^\text{o}$ angle and rotate $153^\text{o}$, you are facing in the same direction you started in, so you have turned through a total of $360^\text{o}$.
You have also turned forwards through the green angles and backwards through the red angles, so the sum of the green angles subtract the sum of the red angles must be $360^\text{o}$. $$\begin{align}154 - 105 + 153 + 156 + -(180 - x ) + 157 &= 360\\
\Rightarrow 515-180+x&=360\\
\Rightarrow 515+x&=540\\
\Rightarrow x&=25\end{align}$$
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

