Skip over navigation
Answer: 37 metres
Using scale factors
Red track - when Anna finishes Blue track - Bridgit and Carol
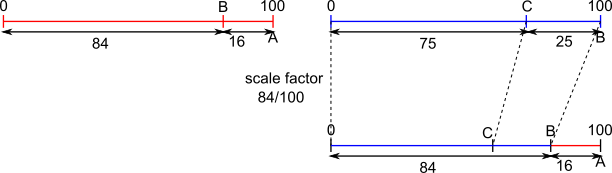
$\frac{84}{100}\times 75 = 84\times \frac34 = 63$
Carol has run $63$ metres when Anna finishes so has $37$ metres left.
Using ratio
The ratio of the distance Anna runs to the distance Bridgit runs in a given amount of time is 100 : 84, because Bridgit has run 100 $-$ 16 = 84 m when Anna finishes the race.
The ratio of the distance Bridgit runs to the distance Carol runs in a given amount of time is 100 : 75, because Carol has run 100 $-$ 25 = 75 m when Bridgit finishes the race.
By expressing this second ratio so that it begins in 84, we can express these two ratios as a single ratio. 100$\div$25$\times$21 = 84, and 75$\div$25$\times$21 = 63, so the ratio 100 : 75 is equivalent to the ratio 84 : 63.
So the ratio of the distance Anna runs to the distance Bridgit runs to the distance Carol runs in a given amount of time is 100 : 84 : 63.
So Carol runs 63 m in the time it takes Anna to run 100 m, so she is 100$-$63 = 37 m behind Anna when Anna finishes the race.
Using proportion
When Anna finished the race, Bridgit had run $100-16=84$m, which is $\dfrac{84}{100}=\dfrac{21}{25}$ of the race. So Bridgit runs at $\dfrac{21}{25}$ of the speed Anna runs at.
When Bridgit finished the race, Carol had run $100-25=75$m, which is $\dfrac{75}{100}=\dfrac{3}{4}$ of the race. So Carol runs at $\dfrac{3}{4}$ of the speed Bridgit runs at.
So Carol runs at $\dfrac{3}{4}$ of $\dfrac{21}{25}$ of the speed Anna runs at, which is $\dfrac{3}{4}\times\dfrac{21}{25}=\dfrac{63}{100}$ of the speed Anna runs at. So when Anna has run $100$m, Carol has run $63$m.
Note that this method can also be done with time, ie. Anna takes $\dfrac{21}{25}$ of the time Brigit takes, etc.
Using a distance-time graph
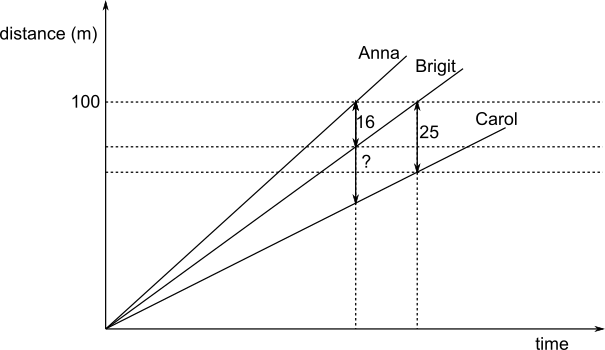
The information in the question is shown on this distance-time graph:
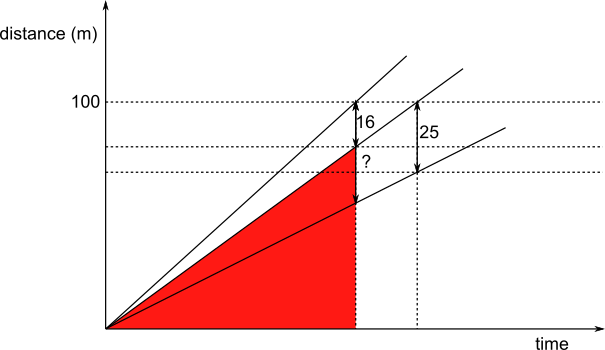
The diagrams below are smaller copies of the one above with similar triangles drawn on. The scale factor between the two red triangles is the same as the scale factor between the two yellow triangles, since the bases of the red triangles are equal to the bases of the yellow triangles.
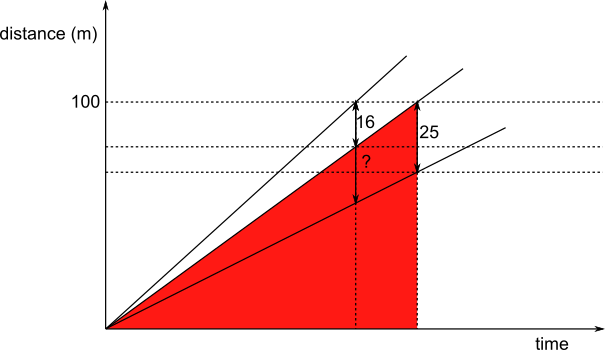

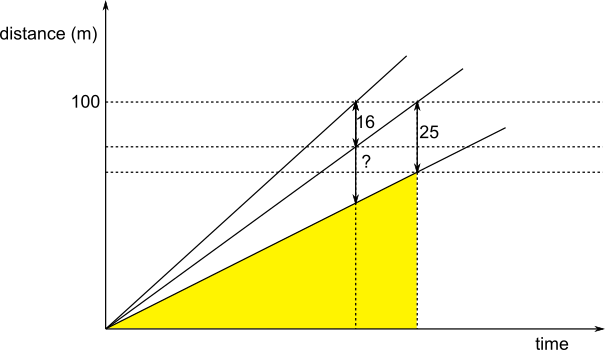
The larger red triangle has height $100$ and the smaller one has height $100-16 = 84$, so the scale factor between the larger red triangle and the smaller red triangle is $\frac{84}{100}=\frac{21}{25}.$
The larger yellow triangle has height $100-25=75$, so the smaller yellow triangle has height $\frac{21}{25}\times75=63$m.
So Carol is $100=63=37$m behind Anna when Anna finishes the race.
Using algebra and the speed-distance-time relationship
Let Anna, Bridgit and Carol run at speeds $a,b,c$ metres per second respectively, and suppose it takes Anna $t_A$ seconds and Brigit $t_B$ seconds to complete the race.
Distance = speed $\times$ time taken, and since Bridgit is $16$ metres behind Anna when Anna completes the race, she runs $100-16=84$ metres in $t_A$ seconds, so $84=bt_A.$ Also, $100=bt_B.$ Similarly for Carol, $100-25=75$ so $75=ct_B.$ We want to know how far behind Anna Carol is when Anna finishes the race, so we need $ct_A.$
Using substitution
$100=bt_B\Rightarrow b=\dfrac{100}{t_B},$ and substituting into $84=bt_A$ gives $84=\dfrac{100}{t_B}t_A\Rightarrow84t_B=100t_A\Rightarrow t_B=\dfrac{100}{84}t_A\Rightarrow t_B=\dfrac{25}{21}t_A$
Substituting into $75=ct_B$ gives $75=c\times \dfrac{25}{21}t_A\Rightarrow \dfrac{75\times 21}{25}=ct_A\Rightarrow63=ct_A.$ So Carol has run $63$ metres when Anna finishes the race, which means she is $100-63=37$ metres behind.
Using algebraic manipulation
'Dividing' $84=bt_A$ by $100=bt_B$ gives $\dfrac{84}{100}=\dfrac{bt_A}{bt_B}\Rightarrow\dfrac{21}{25}=\dfrac{t_A}{t_B}$
'Multiplying' $75=ct_B$ by $\dfrac{21}{25}=\dfrac{t_A}{t_B}$ gives $75\times \dfrac{21}{25}=ct_B\times\dfrac{t_A}{t_B}\Rightarrow63=ct_A.$ So Carol has run $63$ metres when Anna finishes the race, which means she is $100-63=37$ metres behind.
Using the speed-distance-time relationship and fewer variables
At the point when Anna finishes, let Carol be at $x$ metres behind Bridgit. Let the total time taken for Anna to finish be $T$.
Then using speed = distance $\div$ time taken, Bridgit has speed $\dfrac{100-16}{T} = \dfrac{84}{T}$ and Carol has speed $\dfrac{84-x}{T}$.
So, using time taken = distance $\div$ speed, the time taken for Brigit to finish is $\dfrac{100}{\frac{84}{T}}=\dfrac{100T}{84}=\dfrac{25T}{21}$
Using distance = speed $\times$ time taken, in this time Carol travels $\dfrac{84-x}{T} \times \dfrac{25T}{21}$, so, since she is $25$ metres behind Brigit when Bridgit finshes, $$\begin{align}&\dfrac{84-x}{T} \times \dfrac{25T}{21} = 100 - 25\\
\Rightarrow&\dfrac{(84-x)\times25T}{T\times21}=75\\
\Rightarrow&\frac{(84-x)\times25}{21}=75\\
\Rightarrow&\frac{84-x}{21}=\frac{75}{25}=3\\
\Rightarrow&84-x=3\times21=63\\
\Rightarrow &84-63=x=21\end{align}$$
So Carol is $21+16 = 37$m behind the line when Anna crosses it.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
100m Sprint
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: 37 metres
Using scale factors
Red track - when Anna finishes Blue track - Bridgit and Carol

$\frac{84}{100}\times 75 = 84\times \frac34 = 63$
Carol has run $63$ metres when Anna finishes so has $37$ metres left.
Using ratio
The ratio of the distance Anna runs to the distance Bridgit runs in a given amount of time is 100 : 84, because Bridgit has run 100 $-$ 16 = 84 m when Anna finishes the race.
The ratio of the distance Bridgit runs to the distance Carol runs in a given amount of time is 100 : 75, because Carol has run 100 $-$ 25 = 75 m when Bridgit finishes the race.
By expressing this second ratio so that it begins in 84, we can express these two ratios as a single ratio. 100$\div$25$\times$21 = 84, and 75$\div$25$\times$21 = 63, so the ratio 100 : 75 is equivalent to the ratio 84 : 63.
So the ratio of the distance Anna runs to the distance Bridgit runs to the distance Carol runs in a given amount of time is 100 : 84 : 63.
So Carol runs 63 m in the time it takes Anna to run 100 m, so she is 100$-$63 = 37 m behind Anna when Anna finishes the race.
Using proportion
When Anna finished the race, Bridgit had run $100-16=84$m, which is $\dfrac{84}{100}=\dfrac{21}{25}$ of the race. So Bridgit runs at $\dfrac{21}{25}$ of the speed Anna runs at.
When Bridgit finished the race, Carol had run $100-25=75$m, which is $\dfrac{75}{100}=\dfrac{3}{4}$ of the race. So Carol runs at $\dfrac{3}{4}$ of the speed Bridgit runs at.
So Carol runs at $\dfrac{3}{4}$ of $\dfrac{21}{25}$ of the speed Anna runs at, which is $\dfrac{3}{4}\times\dfrac{21}{25}=\dfrac{63}{100}$ of the speed Anna runs at. So when Anna has run $100$m, Carol has run $63$m.
Note that this method can also be done with time, ie. Anna takes $\dfrac{21}{25}$ of the time Brigit takes, etc.
Using a distance-time graph
The information in the question is shown on this distance-time graph:

The diagrams below are smaller copies of the one above with similar triangles drawn on. The scale factor between the two red triangles is the same as the scale factor between the two yellow triangles, since the bases of the red triangles are equal to the bases of the yellow triangles.




The larger red triangle has height $100$ and the smaller one has height $100-16 = 84$, so the scale factor between the larger red triangle and the smaller red triangle is $\frac{84}{100}=\frac{21}{25}.$
The larger yellow triangle has height $100-25=75$, so the smaller yellow triangle has height $\frac{21}{25}\times75=63$m.
So Carol is $100=63=37$m behind Anna when Anna finishes the race.
Using algebra and the speed-distance-time relationship
Let Anna, Bridgit and Carol run at speeds $a,b,c$ metres per second respectively, and suppose it takes Anna $t_A$ seconds and Brigit $t_B$ seconds to complete the race.
Distance = speed $\times$ time taken, and since Bridgit is $16$ metres behind Anna when Anna completes the race, she runs $100-16=84$ metres in $t_A$ seconds, so $84=bt_A.$ Also, $100=bt_B.$ Similarly for Carol, $100-25=75$ so $75=ct_B.$ We want to know how far behind Anna Carol is when Anna finishes the race, so we need $ct_A.$
Using substitution
$100=bt_B\Rightarrow b=\dfrac{100}{t_B},$ and substituting into $84=bt_A$ gives $84=\dfrac{100}{t_B}t_A\Rightarrow84t_B=100t_A\Rightarrow t_B=\dfrac{100}{84}t_A\Rightarrow t_B=\dfrac{25}{21}t_A$
Substituting into $75=ct_B$ gives $75=c\times \dfrac{25}{21}t_A\Rightarrow \dfrac{75\times 21}{25}=ct_A\Rightarrow63=ct_A.$ So Carol has run $63$ metres when Anna finishes the race, which means she is $100-63=37$ metres behind.
Using algebraic manipulation
'Dividing' $84=bt_A$ by $100=bt_B$ gives $\dfrac{84}{100}=\dfrac{bt_A}{bt_B}\Rightarrow\dfrac{21}{25}=\dfrac{t_A}{t_B}$
'Multiplying' $75=ct_B$ by $\dfrac{21}{25}=\dfrac{t_A}{t_B}$ gives $75\times \dfrac{21}{25}=ct_B\times\dfrac{t_A}{t_B}\Rightarrow63=ct_A.$ So Carol has run $63$ metres when Anna finishes the race, which means she is $100-63=37$ metres behind.
Using the speed-distance-time relationship and fewer variables
At the point when Anna finishes, let Carol be at $x$ metres behind Bridgit. Let the total time taken for Anna to finish be $T$.
Then using speed = distance $\div$ time taken, Bridgit has speed $\dfrac{100-16}{T} = \dfrac{84}{T}$ and Carol has speed $\dfrac{84-x}{T}$.
So, using time taken = distance $\div$ speed, the time taken for Brigit to finish is $\dfrac{100}{\frac{84}{T}}=\dfrac{100T}{84}=\dfrac{25T}{21}$
Using distance = speed $\times$ time taken, in this time Carol travels $\dfrac{84-x}{T} \times \dfrac{25T}{21}$, so, since she is $25$ metres behind Brigit when Bridgit finshes, $$\begin{align}&\dfrac{84-x}{T} \times \dfrac{25T}{21} = 100 - 25\\
\Rightarrow&\dfrac{(84-x)\times25T}{T\times21}=75\\
\Rightarrow&\frac{(84-x)\times25}{21}=75\\
\Rightarrow&\frac{84-x}{21}=\frac{75}{25}=3\\
\Rightarrow&84-x=3\times21=63\\
\Rightarrow &84-63=x=21\end{align}$$
So Carol is $21+16 = 37$m behind the line when Anna crosses it.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Bendy Quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.

